-
04-1 척도데이터 분석/파이썬으로 배우는 데이터 분석을 위한 통계학 2022. 3. 17. 15:17
'척도(scale)'란 말 그대로 대상을 관측한 속성값을 타나내는 도구야. 그런데 관찰 대상이 같더라도 관측한 속성값은 다를 수 있어. 다양한 국가와 인종이 있는 만큼 척도도 다양 할 수 있지! 그래서 '표준척도(standard scale)'가 필요해. 척도의 표준을 맞춰야만 상대적으로 비교하기 쉽겠지?
그러나 미국 사람들은 표준척도에 대해서 아는 척도 하면 안 돼. 거기는 척도가 개판이거든.
미터법에서 물 1mL의 부피가 1cm³이고, 질량이 1g이며, 온도를 1℃ 올리는 데 에너지 1 cal가 필요해. 여기서 1℃는 물의 어는점과 끓는점 간극의 1%를 말하지. 또한, 수소 1g에 들어있는 수소원자의 양은 정확히 1 mol이야.
반면 미국의 단위계에서 '물 1갤런을 끓이기 위해 얼마나 많은가?'라는 질문에 대답은 '좆까라. (Go fuck your self.)'인데, 미국 단위계에서는 각각의 물리량들 사이에서 직관적인 상관관계를 찾을 수 없기 때문이지. (갑자기 욕이 나와서 당황스럽지만 책 내용을 그대로 발췌했어!)
조시 베젤의 책 와일드 싱(Wild Thing)의 내용 중에 나오는 글이야.
왜 미국의 단위계는 개판이 되었을까? 그냥 예부터 써오던 과학적이지 않은 단위를 별 생각없이 현대에 이르기까지 쓰고 있기 때문이지 뭐. 그럼 이러한 불편을 감수하면서 살아야 할까?
통계학에서는 '표준점수(standard score)'를 사용해 표준척도를 만들어 개판인 단위계를 하나의 기준으로 비교 분석하게 만들 수 있어!
미국을 비롯한 극소수의 국가에서만 쓰이는 온도의 단위인 화씨(°F)를 살펴볼까? 우리는 섭씨(℃)를 쓰고 있으니 화씨에 익숙하지 않겠지만 말야. 화씨와 섭씨는 온도를 측정하는 두 개의 서로 다른 척도지. 그래서 화씨 0도와 섭씨 0도는 같은 수치를 나타내지만 실제로 다른 온도가 돼. 만약 섭씨를 화씨로 바꾸고 싶다면 섭씨 온도에 1.8을 곱한 다음 32를 더하면 돼. 복잡하지?
°F = 1.8×℃+32
섭씨 척도에서는 0도에서 물이 얼고 100도에서 물이 끓지만 화씨 척도에서는 32도에서 물이 얼고 212도에서 물이 끓을거야. 중요한 것은 변환 공식에 1.8과 32라는 상수가 있다는거야. 1.8을 곱해주고 32를 더해야만 섭씨가 화씨로 변환될 수 있어.

섭씨를 화씨로 기존 척도 단위에 상수를 곱하거나 더해주어서 서로 다른 두 척도에 대한 이해가 가능해 졌지!
그러나!
수치가 달라졌다고 해서 본질적인 온도가 변한 것은 아니야. 섭씨를 화씨로 나타낸다고 해서 원래 섭씨 0도에서 얼어야 할 물이 더 높은 온도에서 얼지 않을 것이고, 화씨를 섭씨로 나타낸다고 해서 원래 화씨 212도에서 끓어야 할 물이 더 낮은 온도에서 끓지 않을거야. 수치만 달라지 것 뿐이지.
이 밖에도 미국에서 주로 쓰는 인치, 피트, 마일, 온즈, 갤런.. 등 아주 거지같은 단위들이 많이 있어. 오죽하면 세계적으로 널리 쓰이는 단위가 미국에서 다르게 쓰이는 바람에 로켓 엔진이 폭발하고 비행기가 불시착하는 경우도 있지. 척도가 표준화되어있지 않은 경우에 발생할 수 있는 최악의 상황들이 될거야.
계속 강조하지만 이 글의 요지는 눈에 보이는 절대적인 수치가 다가 아니라는 거야.
예를들어 수학 시험을 봤는데 90점을 맞았다고 해 볼게. 영어는 60점을 맞았고. 그럼 수학 시험을 잘 본 것이라고 말할 수 있을까? 또는 영어 시험을 못 본 것이라고 말할 수 있을까?
못 해!
수학 시험이 너무 쉬워서 다른 친구들은 대부분 100점이나 95점 이상이라면 내가 맞은 90점이라는 점수가 굉장히 낮은 점수일수도 있거든. 혹은 영어 시험이 너무 어려워서 다른 친구들은 20점 30점인데 나만 60점이라면 내 점수가 굉장히 높은 점수가 되겠지?
그래서 표준점수가 필요한거야. 표준점수에 대해 본격적으로 다뤄보기전에 표준척도에 대해 다시 이야기 해 볼게.
섭씨를 화씨로 변환했던 것 처럼 척도는 변환할 수 있어. 하지만 척도가 변환한다고 해서 본질이 바뀌는 것은 아니야. 만약 국어 시험의 문제가 출제자의 실수로 잘못 출제되었다고 생각해 볼게. 그래서 추후 논란을 없애기 위해 해당 문제는 모든 학생들에게 정답처리를 하기로 했어. 내 원래 국어 점수가 75점이고 해당 문제가 5점이라면 80점이 되는거지. 75점에서 80점이 되었으니 성적이 오른 것일까? 아니야. 그대로야. 나만 5점 오른게 아니라 다른 모든 학생들도 5점이 올랐거든.
만약 1학년 학생들의 평균 국어 시험 점수가 70점 이었다고 가정해 볼게. 오류로 인해 정답처리를 한 다음의 평균은 어떻게 될까? 5점짜리 문제였으니 당연히 학생들의 평균 점수는 5점이 올라서 75점이 될거야. 당연하지? 기존 평균 점수를 m이라 하고, 새로운 평균 점수를 m'라 할게. 그리고 평균에 더해지는 상수는 c로 표현해서 나타내면
m' = m+c
라고 나타낼 수 있어. 그림으로 나타내면?
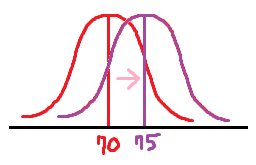
분포는 갖지만 평균이 상수만큼 증가하는 식으로 나타낼 수 있을거야.
또, 상수를 더하거나 빼지 않고 곱하거나 나눌 수도 있겠지. 평균이 m(X바)라 하고 상수를 곱해준 새로운 평균이 m'(X'바)라 했을 땐,

이와 같이 쫘악 넓어진 분포를 볼 수 있을거야. 대신 평균은 변하지 않겠지. 수식으로 나타내면
m' = m×c
로 나타낼 수 있어.
물론 상수를 더하거나 뺀 다음 곱하거나 나눌 수도 있을거야. 우리가 섭씨 온도를 화씨 온도로 변환했던 것 처럼. 가능하겠지?
위 그림처럼 모든 점수들에 상수를 더하거나 빼주면 원점이 변경돼. 모든 점수들에 같은 상수값을 더하거나 빼주면 당연히 점수들의 평균도 그 상수만큼 더하거나 빼주면 되겠지?
그리고 모든 점수들에 상수를 곱하거나 나눠주면 단위가 변경돼. 마찬가지로 모든 점수들에 같은 상수값을 곱하거나 나눠주면 당연히 점수들의 평균도 그 상수만큼 곱하거나 나눠주면 될 거야.
그리고 둘 다 같이 해주면 원점도 변경되고 단위도 변경되겠지.
이렇게 척도를 변환했을 때 평균이 어떻게 변하는지는 알기 쉬웠어.
그럼 척도를 변환했을 때 분산과 표준편차는 어떻게 될까?
먼저 상수를 더하거나 빼서 원점이 변경된 경우부터 생각해 볼게. 1학년 학생들의 국어 시험 평균 점수가 70점 이었는데, 출제자의 실수로 5점짜리 문제가 정답처리되어 75점으로 바뀌는 경우를 다시 살펴볼까?
내 점수가 5점 올랐어. 눈에 보이는 수치는 오른 것이지. 하지만 다른 모든 학생들의 점수도 같이 올랐기 때문에 결국 오르지 않은것이나 마찬가지가 될거야. 왜? 평균과의 차이가 그대로거든. 바뀌기 전 내 시험 점수가 75점 이었다면 1학년 학생들의 평균 점수 70점 보다 5점이 많았어. 그리고 5점 짜리 문제가 정답처리 된 다음에는 내 점수가 80점이 되었지만 1학년 학생들의 평균 점수도 5점이 올라서 75점이 된 것이지. 평균과 내 점수의 차이는? 그대로야. 5점.
분산의 개념을 다시 떠올려보면, 분산은 '내 점수가 평균으로부터 떨어진 면적'이라고 했어. 그런데 상수가 더해지기 전이나 후나 평균과의 차이가 같다면 분산도 역시나 같겠지? 당연히 분산의 제곱근인 표준편차도 같을 수 밖에 없고 말야. 너무 당연한가? 기존 분산을 s²라 하고, 상수 c를 더한 새로운 분산을 s'²라 했을 때 증명을 하면서 다시 살펴볼게.
s'² = s² 증명 연산 설명 ⓐ s'² = s² = ∑{(x+c)-(m+c)}² / (N-1) ⓐ 모든 점수치들에서 상수를 더한 것과 평균에서 상수를 더한 것들의 제곱의 합을 N-1로 나눠서 분산을 구함. ⓑ = ∑(X+c-m-c)² / (N-1) ⓑ 중괄호 벗김. ⓒ = ∑(X-m)² / (N-1) ⓒ 상수 c가 제거 됨. 증명을 살펴보니 훨씬 더 명확해 졌어. 상수를 더하거나 뺀다고 해도 분산이나 표준편차는 달라지지 않지! 꼭 기억해야 돼!
그럼 상수를 곱해서 단위를 변경하면 어떻게 될까?
ㅇㅇ만약 1학년 학생들의 국어 시험 평균 점수가 70점 이었는데, 모든 학생들의 점수를 두 배로 늘리기로 했어. 140점이 되는거야. 내 점수가 75점 이었다면 150점이 되겠지? 이전에는 평균과의 차이가 5점이었는데, 점수가 두 배로 되니 10점 차이가 되었어. 앗! 평균과 내 점수의 차이를 뜻하는 분산은 당연히 변하겠구나! 라는 생각이 들지?
그런데 정확히 어떤 변화가 있을까?
간단해. 점수들이 c배 늘어나면 표준편차도 c배 늘어나. 표준편차의 제곱인 분산은 c²배 늘어날 것이고. 내 점수와 평균과의 차이가 5점이었는데 점수들이 두 배가 되면서 내 점수와 평균과의 차이가 10점이 되었잖아? 10점은 5점의 두 배이지. 표준편차도 당연히 두 배 늘어날거고 말야. 확인해 볼까? 마찬가지로 기존 분산을 s²라 하고, 상수 c를 곱한 새로운 분산을 s'²라 했을 때 증명해 볼게.
s'² = c²s² 증명 연산 설명 ⓐ s'² = c²s² = ∑{(cx)-(cm)}² / (N-1) ⓐ 모든 점수치들에서 상수를 곱한 것과 평균에서 상수를 곱한 것들의 제곱의 합을 N-1로 나눠서 분산을 구함. ⓑ = ∑{c(x-m)}² / (N-1) ⓑ cx-cm = c(x-m) 인수분해 ⓒ = ∑c²(x-m)² / (N-1) ⓒ c(x-m)² = c²(x-m)² 단순화 ⓓ = c²∑(x-m)² / (N-1) ⓓ 점수를 상수배해서 합한 값과 점수를 합하고 상수배 한 것은 같음. ⓔ = c² { ∑(x-m)² / (N-1) } = c²s² ⓔ ∑(x-m)² / (N-1) 을 분산 s²로 치환. ⓕ s'² = c²s²
∴ s' = √(c²s²) = csⓕ 분산에 루트를 취해서 표준편차를 구함. 어떻게 보면 당연한 이야기지만 증명을 통해 과정을 보니 더 쉽게 이해할 수 있네!
척도가 변환되면서 원점이나 단위가 변하고 이에 따라 평균과 분산 그리고 표준편차에 어떻게 영향을 미치는지 이제 알겠지? 알아야 돼.. 그래야 앞서 말했던 표준점수에 대해 말할 수 있거든..! 안뇽!
'데이터 분석 > 파이썬으로 배우는 데이터 분석을 위한 통계학' 카테고리의 다른 글
04-3 파이썬으로 표준화 (0) 2022.03.17 04-2 표준화와 표준점수 (0) 2022.03.17 03-8 모집단과 표본집단 : 모수치와 통계치 (0) 2022.03.17 03-6 변산성의 지표 1 : 분산과 자유도 (0) 2022.03.17 03-5 중심경향의 지표들과 파이썬 : 라이브러리와 모듈 (0) 2022.03.16