04-6 표준정규분포의 넓이와 백분위 그리고 표준정규분포표

 여태까지 표준화를 하기 위해 많은 연습들을 해 왔어. 그리고 어떤 데이터라도 표준화를 한다면 평균이 0, 표준편차가 1이 된다는것도 알았지. 그럼 평균이 0이고 표준편차가 1이라는 것 이외에 무엇을 알수 있을까?

 

 통계에 대해 공부하기 위해서는 '확률'에 대해 알아야 돼. 그래서 고등학교 땐 '확률과 통계'로 배우잖아. 줄여서 확통! 그 만큼 통계와 확률이 밀접한 관계를 가지고 있기 때문이야. 그리고 확률에 대해 떠올려보면 전체는 100%라는 개념이 떠 오를거야. 바꿔 말하면 전체는 1이지. 어? 표준정규분포 또한 표준편차가 1인데? 1이라는 숫자가 자주 등장하는거 보니 또 무언가 연관성이 있지 않을까?

 

 우리는 여러가지 통계적 지표들을 배워오면서 절대적인 수치보다 중요한 것은 상대적인 의미라는 것을 알게 되었어. 내 시험 점수가 낮다고 생각되어도 평균점수 또한 낮다면 그리 나쁜 점수가 아닐 수 있다는 것을 알잖아. 통계에서는 상대적 의미가 중요해. 그리고 상대적 의미는? 전체를 100%, 즉 1로 놓고 비교하면 편하게 알 수 있었지. 앞서 상대빈도에 대해 배웠을 때 다뤘었지?

 

https://kimhaksung.tistory.com/entry/pytong02-1 

02-1 분포의 특징 : 빈도분포와 상대빈도분포

 

 상대빈도에서는 전체를 1로 놓았었어. 왜? 비교가 쉽기 때문이지. 그리고 확률에서도 전체를 1로 놓잖아. 왜? 알기 쉬우니까! 그리고 우리가 알게 된 표준정규분포도 전체가 1이야. 왜? 알기 쉬우니까!

 

 

 위 표준정규분포 그래프의 파란색 총 면적이 1이라는 뜻이야. 당연히 절반의 넓이는 0.5가 되겠지?

 

 

만약 내 표준점수를 알면 내가 전체에서 얼마만큼의 백분위에 해당되는지 알 수 있게 돼. 표준점수 까지의 넓이가 백분위를 뜻 하거든.

 

 그럼 해당 표준점수의 백분위를 알 수 있어. 어떻게?

 

 

 표준정규분포의 면적 비율은 이미 다 정해져 있거든! 위 정규분포를 보면 각각의 색깔들은 해당 면적의 넓이를 뜻 해. 표준점수 1과 사이의 면적은 약 0.1359 인것이지! 이 넓이는 내가 정한게 아니라 '표준정규분포표'에 따른거야. 표준정규분포표는 아래의 링크를 참고하면돼.

https://ko.wikipedia.org/wiki/표준정규분포표

표준정규분포표 - 위키백과, 우리 모두의 백과사전

 

 만약 내 표준점수가 1이라면 표준점수 아래의 있는 면적들의 합이 내 백분위가 되는거야.

 

 

 내 표준점수가 1이라면 내 백분위는 0.0013과 0.0215와 0.1359와 0.3413, 마지막으로 0.3413을 더한 값이 되겠지? 약 0.8413이될거야. 표준점수 1점은 백분위 84.13%라는 뜻이지. 대충 100명 중에 84등 이라는 뜻이야. 표준화를 했더니 표준정규분포에 이를 수 있었고 백분위를 구하는게 쉬워졌지? 넘 좋당!

 

-

 

 원점수로 생각해 볼까? 만약 평균 점수가 50, 표준편차가 10인 시험에서 나는 60점을 받았다고 해 볼게. 나는 시험을 잘 본 것일까? 내 점수의 백분위는 얼마나 될까?

 

 일단 원점수를 표준점수로 바꿔주어야 돼. 내 점수와 평균의 차이에서 표준편차를 나눠주면 표준점수가 나오겠지. 60에서 50을 빼고 10으로 나눠주면? 1점! 내 표준점수는 1점이야. 그렇다면 내 백분위는? 위의 그림과 같아. 0.8413이지. 약 100명 중 84등이야. 60점이라고 해서 시험을 잘 못 본줄 알았는데 평균과 표준편차를 고려했더니 꼭 그렇지만은 않지?

 

 

 내 표준점수의 백분위가 몇 인지는 표준정규분포표의 숫자를 보고 읽기만 하면되니까 너무 쉬워. 아마 초등학생도 쉽게 할 수 있을거야.

 

 

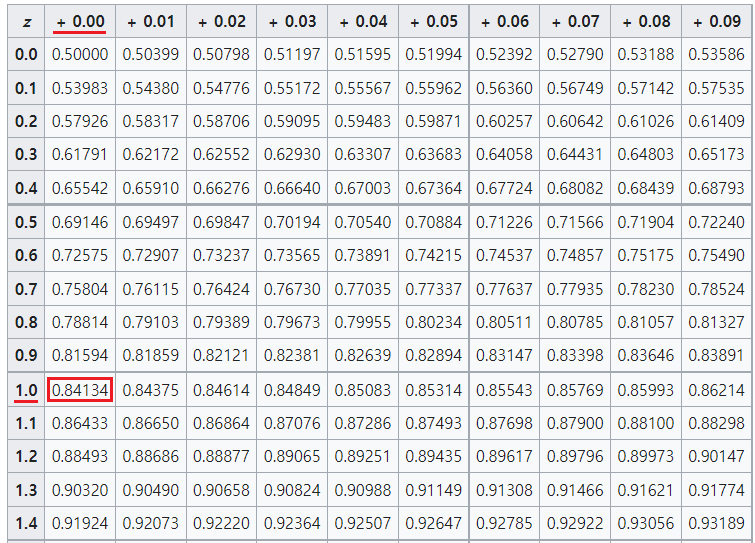
 표준점수가 1.00일 땐 먼저 표의 왼쪽에서 1.0을 찾으면 돼!

 찾았어?? 이제 1.0 뒤에 있는 숫자를 볼텐데.. 1.0은 사실 1.000 으로 써도 되잖아? 뒤에 00이니까 표의 맨 위로 가서 0.00을 찾으면 돼! 이제 왼쪽과 위쪽의 교차되는 숫자를 찾기만 하면? 끝!

0.84134 라고 표준정규분포표에 나와있으니 우린 이걸 그냥 가져다 쓰기만 하면 돼. 엄청 쉽지!

 

-

 

 그럼 혹시 파이썬을 활용하면 쉽게 표준점수에 해당되는 백분위를 구할 수 없을까?

 있어!

 다만, 표준정규분포표를 파이썬으로 만들 순 없으니까 표준정규분포표의 데이터가 포함되어있는 라이브러리를 사용할거야. 저번에 한 번 사용해 봤던 'scipy' 라이브러리 말야!

 

 scipy 라이브러리를 활용하면 쉽게 표준점수의 백분위를 알 수 있어.

 이번에는 우리가 직접 표준점수를 입력해 보면서 백분위를 알아 볼거야. 사용자가 어떤 값을 입력할 땐 'input()' 이라는 함수를 사용해.

 

input(입력안내)

 

 소괄호 안은 비워두어도 되지만 되도록이면 사용자가 어떤 것을 입력해야 되는지 알려주면 좋아. 아래의 코드처럼 말야.

 

 

 위 코드는 사용자로부터 값을 입력받고 'Z_score'라는 변수에 담았어. 그리고 Z_score를 출력했고 말야. 그런데 여기서 잘 봐야 될 것은 사용자가 입력한 값의 '자료형(type)'이야. 만약 여러분이 숫자를 입력했으면 숫자가 출력될 것이고, 문자를 입력했으면 문자가 출려될거야. 그치?

 아니야.

 여러분이 숫자를 입력하던, 문자를 입력하던 출력된 놈은 문자야.

 어떻게 알 수 있냐고? 아래의 코드를 실행해 보면 돼!

 

 

 위의 코드를 실행해 보면 숫자를 입력하든 문자를 입력하든 '<class 'str'>'이라고 출력되는 것을 볼수 있어. 'str'은 'string'의 약자야. '문자열'이라는 뜻이지. 숫자를 입력하고 출력 결과를 봐도 숫자처럼 보이지만 사실은 문자열인거야. 그럼 어떡하지? 숫자로 바꿔주면 돼!

 

 전에 한 번 'int()' 함수에 대해 배운적이 있었어. 소괄호 안의 숫자를 정수로 바꿔주는 함수였지. 하지만 표준점수는 항상 정수가 아닐것이기 때문에 값을 실수로 바꿔주는 'float()' 함수를 사용할거야. 사용자가 입력한 값의 float()를 씌워서 실수로 바꿔볼까?

 

 

이번에는 '<class 'float'>'가 출력된 것을 볼 수 있어. 이제 이 표준점수의 백분위를 알아볼거야. 저번처럼 scipy 라이브러리의 stats 모듈을 사용할거야. stats 모듈에서 정규분포를 뜻 하는 'norm'의 'cdf()' 함수를 사용할거야. cdf() 함수는 '누적분포함수(cumulative distribution function)'의 약자야. 우리는 해당 표준점수의 누적상대빈도에 따른 백분위를 구할 것이기 때문에 cdf() 함수를 사용하면 백분위를 구할 수 있어. 말은 어려워 보이지만 코드로 나타내면 간단하니 아래의 코드를 볼까?

 

 

 어때? 표준점수로 1을 입력했더니 약 0.8413이 출력되는 것을 볼 수 있어. 우리가 원하던 표준점수에 따른 백분위가 이렇게 쉽게 출력되다니! 넘 좋지? 숫자가 너무 더럽다고 생각되면 round() 함수를 사용해서 반올림하면 될거야.

 

 이제 표준화를하는 이유, 표준정규분포의 의미를 알겠지? 중요한 것은 어떤 분포라도 표준화를 할 수 있긴 하지만 오직 정규분포만이 표준정규분포가 될 수 있다는 것이야. 막 이상한 분포를 가지고 와서 왜 표준화 했는데 표준정규분포가 안되냐고 하면 안돼! 안뇽!