06-2 상관 계수의 유도 : 피어슨 상관 계수, r (feat. 전설의 통계학자들)

 드디어 나온 그 이름! 피! 어! 슨! 오늘은 칼 피어슨(Karl Pearson)의 상관 계수(또는 적률 상관 계수), r에 대해 다뤄볼 거야. 이 집안은 통계학을 다 해먹는 집안이라 우리가 꼭 알아야 하는 가문이야.

 통계학에서 칼 피어슨이 왜 중요하냐면.. 대학의 '통계학과'를 세계 최초로 설립한 인물이기 때문이야. 말 그대로 통계학의 아버지이자 어머니 그야말로 통계학의 마더파더.. 그저 갓.. 찬양..

 

 칼 피어슨에 대해 살펴보기 전에 우리가 통계학에서 기억해야 하는 인물들을 시대 순으로 정리하고 갈까? 공부 하다보면 이런게 재밌지.. 대신 기원전 인물들 까지 다루면 넘 많이질거 같으니까 기원후로만 다뤄볼게.

 

-

 

전설의 통계학자들

 

 1. 요한 카를 프리드리히 가우스 (Johann Carl Friedrich Gauß) 1777.4.30-1855.2.23

 가우스는 내가 특히나 좋아하는 수학자인데, 프로그래밍을 가르칠 때 가우스가 고안해 낸 방법을 코드로 구현하도록 실습하는 것이 학생들에게 놀라운 경험이 되기 때문이야. 특히 가우스는 우리가 통계학을 배우면서 계속 써먹고 있는 '최소 제곱법'을 최초로 고안해 냈기 때문에 우리가 통계학을 배우면서 꼭 알야아 하는 인물 중 하나이지. 최소 제곱법을 써먹을 때 마다 가우스에 대해 기억해 내면 좋겠지? 그 외의 업적들도 너무 많지만.. 우리가 배운 내용과 직접적으로 연관이 있는 인물만 다루고 넘어갈게.

 

 2. 프랜시스 골턴 경 (Sir Francis Galton) 1822.2.16-1911.1.17

 프랜시스 골턴 경에 대해서는 정규분포를 다룰 때 많이 들었었지? '골턴 보드'의 그 골턴 경이야. 특히 찰스 다윈의 사촌으로 '회귀'에 대해 최초로 고안해 낸 인물이지! 찰스 다윈의 유전학적 주장대로 아버지의 키가 크면 자식의 키도 크더라, 하지만 자식은 아버지 만큼 키가 크지 않더라! 이것이 회귀이구나! 기억나지?

 

 3. 칼 피어슨 (Karl Pearson) 1857.3.27–1936.4.27

 드디어 오늘 배울 칼 피어슨이야! 칼 피어슨은 앞서 말한대로 1911년 유니버시티 칼리지 런던에 세계 최초의 대학 통계학과를 설립한 인물이야. 크으.. 칼 피어슨에 대해 배우려면 프랜시스 골턴 경과의 일화를 알아야 돼.

 

 우리는 지금 회귀 분석을 배우면서 '두 변인이 얼마만큼의 차이가 있는가?' 즉, '두 변인의 상관 관계는 어떻게 되는가?'라는 것을 고민하고 있잖아. 왜? 회귀 분석을 하다보니까 회귀선이 점수치들을 얼마나 대표하는지 알고 싶어졌기 때문이지. 우리만 궁금한게 아니야. 회귀에 대한 개념을 고안했던 프랜시스 골턴 경 또한 궁금했어. 자신이 고안해 낸 개념은 맞지만 어떻게 계산을 해야 될지 감이 안왔던 것이지.

 왜냐면 프랜시스 골턴 경은 수학자가 아니라 인류학자였고, 인류학을 기반으로 한 회귀 분석들은 어느 한 변인이 다른 한 변인에게 대부분 영향을 미치고 있었거든.정적인 영향을 미친다는 것이지. 하지만 꼭 모든 경우가 그러진 않았어. 일을 하면 할 수록 돈을 잃는 경우 처럼, 부적인 영향을 미치는 경우도 있었거든. 어느 민족에서는 아버지의 키가 클 수록 자식의 키가 작아진 다던가 하는 경우 말야. 프랜시스 골턴 경은 정적인 상관에 대해서는 0과 1사이의 값으로 상관 관계를 정립할 수 있었지만, 부적인 영향을 미치는 경우에서는 개념을 정립하기가 쉽지 않았던거야.

 

그래서 프랜시스 골턴 경은 당대 최고의 통계학자인 칼 피어슨에게 까지 이 문제가 닿았던 것이지. 어떻게 프랜시스 골턴 경의 문제가 칼 피어슨에게 닿았는지는 모르겠지만, 암튼 칼 피어슨은 두 변인이 정적 상관 관계를 갖고 있던, 부적 상관 관계를 갖고 있던 상관 계수를 계산하여 알 수 있도록 고안해냈어. 그것이 바로 오늘 배울 피어슨 상관 계수 r이야.

 

-

 

 정적 상관 관계와 부적 상관 관계

 

 상관 계수에 대해 공부하기 전에 정적(positive) 상관 관계와 부적(negative) 관계에 대해 배울거야. SAT 점수와 GPA처럼 SAT 점수가 높을 수록 GPA도 높은 경우에는 정적 상관이라고 해. 아래의 고구마는 대략 2시에서 8시 방향으로 기울어져 있잖아. 즉, 기울기가 양수잖아. 이럴 땐 정적 상관 관계가 있다고 해.

 

 자주 등장하는 고구마네! 중요하니까 자주 등장하겠지? 하핫!

 

 반대로 부적 상관 관계는 고구막 기울어진 방향이 반대야. 아래의 그림처럼 말야.

 

 

 즉, 기울기가 음수라는 것이지. 중요한 것은 고구마가 어느 방향으로 기울어졌냐가 아니라! 고구마가 정적이든, 부적이든 뚱뚱할 수록 두 변인의 상관 관계가 약할 것이고, 고구마가 날씬할 수록 두 변인의 상관 관계가 강하다는거야. 우리에게 중요한 것은 정적이냐 부적이냐 보다는 고구마의 모양이야.

 

-

 

상관 계수의 유도

 

 그럼 이제 구체적으로 고구마 모양에 따라 얼마나 상관이 있는지 알아봐야겠지?

 

 우리는 상관 계수를 유도하기 위해 Johny의 사례를 살펴볼거야. 학자들은 Johny 를 포함한 다섯 명의 학생들을 조사했어. 부모의 소득과 아이들의 문해력이 어떤 관계가 있는지 알고 싶었기 때문이야. 주의할 점은, 여러분들은 아마 '부모의 소득이 높으면 아이들의 문해력 또한 높을 것이다.'라고 예측할 수 있겠지만, 우선은 아무런 배경 지식과 고정 관념이 없는 상태에서 출발 했음 좋겠어. 예측하지 말라는 것이지. 통계학적으로 객관적 수치를 먼저 보자고!

 

 아래는 Johny를 포함한 다섯 명의 학생들에 대한 그래프야.

 

 

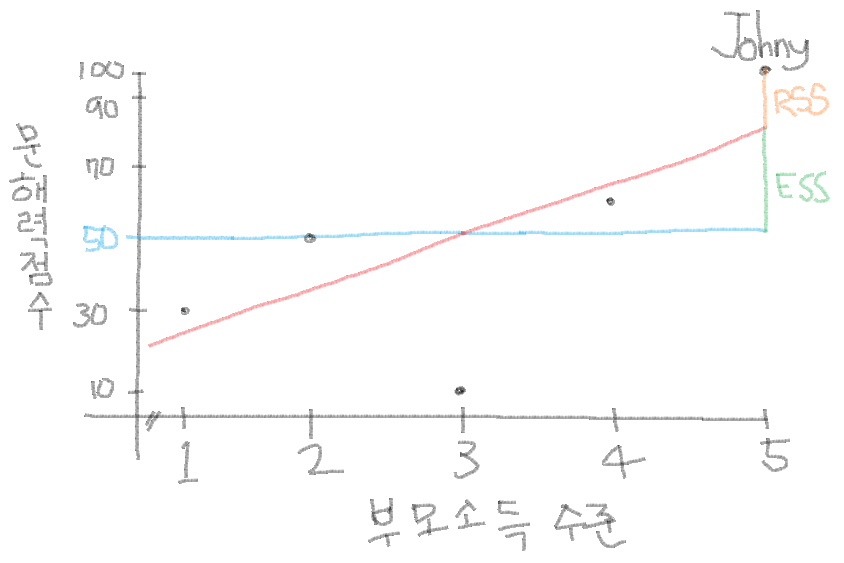
 빨간선은 회귀선, 파란선은 평균선이야. Johny는 유복한 집안에서 태어나 부모의 소득 수준이 굉장히 높았네. 5점 만점이야. 문해력 또한 가장 높은 점수를 받았어. 100점 만점이구먼! 표로 정리해 보면,

Johny의 부모 소득 수준과 문해력 점수
Ym (평균 점수)	Yh (예측 점수)	RSS (Yi-Yh)	ESS (Yh-Ym)	TSS (Yi-Ym, RSS+ESS)
50	80	100-80 = 20	80-50 = 30	100-50 or 20+30 = 50

 

 이제 이 수치(거리)들이 어떤 의미를 가지고 있는지 생각해 볼까? 우선 여러분들에게 문해력 점수(Y) 외에는 아무런 정보가 없는 상태에서 Johny의 문해력 점수를 예측한다고 가정해 볼게. 회귀에 대한 개념이 없다면 당연히 평균으로만 생각할 거야. 대충 Johny의 문해력 점수가 평균 점수인 50점 정도일 것이라고 생각하겠지. 그러나 실제 Johny의 문해력 점수는 100점이기 때문에 50점 만큼이나 틀린 예측을 한 거야. 타당했지만 틀렸지.

 

 다음으로는 부모의 소득 수준(Y)을 알게 되었다고 가정해 볼게. 이제 여러분들은 두 개의 변인을 알게 되었기 때문에 회귀 분석을 할 수 있을거야. 회귀 분석의 결과로 Johny의 점수가 80점이라고 예측할 수 있을거야. 회귀 분석을 했더니 실제 점수 100점이랑 20점 밖에 차이나지 않네! 평균 점수와는 50점이나 차이가 났었는데 말야! 30점이나 줄였어!

 

 이 개념들이 RSS와 ESS 그리고 TSS였지! 저번 시간에 배운 개념이었어.

 

 중요한 것은 TSS(Yi-Ym)가 RSS(Yi-Yh)와 ESS(Yh-Ym)의 합이라거야. 예측하고 남는 차이와 예측해서 줄인 차이를 더하면 원래 전체 차이라는 것이지.

 

Yi-Ym = (Yi-Yh) + (Yh-Ym)

: 전체 차이 = 예측하고 남는 차이 + 예측해서 줄인 차이

 

 점수치에는 Johny만 있는게 아니니까 Johny를 포함한 다른 친구들의 차이도 포함해야 겠지? 이 차이들의 합을 구하려고 하는데 변산을 구할 때 처럼 최소 제곱법에 의해 구할 수 있을거야. RSS와 ESS를 다 더해서 TSS를 구하나, RSS들을 제곱하고 ESS도 제곱해서 다 더한것으로 TSS의 제곱을 구하나 그게 그거잖아? 위의 수식과 아래의 수식이 같다는 것이지.

 

∑(Yi-Ym)² = ∑(Yi-Yh)² + ∑(Yh-Ym)²

: ∑전체 차이² = ∑예측하고 남는 차이² + ∑예측해서 줄인 차이²

: TSS = RSS + ESS

 

 전체 차이의 제곱 합은 예측하고 남은 차이의 제곱 합과 예측해서 줄인 차이의 제곱 합을 더한 것과 같다는 거야.

 

 이때 우리는 전체 차이로 부터 예측해서 줄인 차이의 비율을 알아볼 수 있어.

 

∑예측해서 줄인 차이² / ∑전체 차이²

: ESS / TSS

 

 이 비율만 알면 회귀선이 전체 차이 대비 얼마나 더 잘 예측했는지 알 수 있으니까 말야. 만약 회귀선이 완벽하게 예측했다면 전체 차이와 예측해서 줄인 차이가 같을거야. 왜냐면 원래는 평균만 가지고 예측할 수 밖에 없어서 Yi와 Ym만큼의 차이가 있었는데, 회귀선을 통해 Yh와 Ym만큼의 차이를 줄인거잖아. 즉, 회귀선 상에 점수치가 놓여있다는 것이지! 이렇게 되면 Yi-Ym과 Yh-Ym이 같아지게 되잖아? 그럼 분자가 분모와 같으니 1이 될 수 밖에 없지. 회귀선이 잘 예측할 수록 1에 가까워 지는거야.

 

∑(Yh-Ym)² / ∑(Yi-Ym)²

: ESS / TSS

 

반대로 예측해서 줄인 차이는 전체 차이에서 예측하고 남는 차이를 뺀 것이라고도 할 수 있어. 전체 차이가 예측하고 남는 차이와 예측해서 줄인 차이의 합이니, 예측해서 줄인 차이는 전체 차이에서 예측하고 남는 차이를 뺀 것이 되겠지?

 

∑(Yi-Ym)² = ∑(Yi-Yh)² + ∑(Yh-Ym)²

: ∑전체 차이² = ∑예측하고 남는 차이² + ∑예측해서 줄인 차이²

: TSS = RSS + ESS

에서

∑(Yh-Ym)² = ∑(Yi-Ym)² - ∑(Yi-Yh)²

: ∑예측해서 줄인 차이² = ∑전체 차이² - ∑예측하고 남는 차이²

: ESS = TSS - RSS

 

결과적으로 그놈이 그놈이긴 하나 이를 공식화 해보면

 

∑(Yh-Ym)² / ∑(Yi-Ym)²

: ∑예측해서 줄인 차이² / ∑전체 차이²

: ESS / TSS

= 

{ ∑(Yi-Ym)² - ∑(Yi-Yh)² } / ∑(Yi-Ym)²

: ( ∑전체 차이² -∑예측하고 남는 차이² ) / ∑전체 차이² = 1 - ∑예측하고 남는 차이² / ∑전체 차이²

: ( TSS - RSS ) / TSS = 1 - RSS / TSS

 

 가 되는거지. 좀 복잡해 보이지만 여러분들이 기억할 것은 단 하나야!

 

∑(Yh-Ym)² / ∑(Yi-Ym)²

: ∑예측해서 줄인 차이² / ∑전체 차이²

: ESS / TSS

 

 이거 말야.

 예를 들어서 부모의 소득과 문해력에서 이 비율이 0.55라고 한다면 부모의 소득과 문해력의 전체 차이 중 55%가 부모의 소득과 상관이 있다는거야. 왜? 평균만 봤을 때 보다 부모의 소득이라는 변인이 끼어드니까 55%가 달라졌잖아. 0.55니까. 그러니 55%의 상관이 있다고 말 할수 있는것이지!

 

피어슨 상관 계수, r

 

 하지만 이 비율은 어느정도의 상관 관계는 알려주지만 상관 관계의 방향은 알려주지 않아. 우리는 음수든 양수든 모든 차이들을 제곱해서 다 더했잖아. 양수와 양수를 가지고 비율을 구했는데 어떻게 음수가 나오겠지. 정적 상관 관계는 양수, 부적 상관 관계는 음수가 나와야 할 테인데, 양수만 나오잖아! 그러니 우리는 다시 제곱근을 취해서 상관 관계의 방향성을 알아볼 필요가 있어. 대신 정적 관계라고 하면 양의 제곱근을, 부적 관계라고 하면 음의 제곱근을 취해야 돼.

 이것이 바로 피어슨 상관 계수, r 이야.

 

r² = ∑(Yh-Ym)² / ∑(Yi-Ym)²

r = √{ ∑(Yh-Ym)² / ∑(Yi-Ym)² }

: √( ESS / TSS )

 

당연히 r은 r²에 제곱근이 되겠지? r은 앞서 배운대로 회귀 분석을 통한 예측이 완벽하다면 분모와 분자가 같아서 최대값이 1이 돼. 1은 제곱을 해도, 제곱근을 취해도 1이기 때문에 r의 범위는 0부터 1이 될거야. 하지만 X와 Y의 관계가 부적 관계를 가지고 있다면 음의 제곱근을 취해야 하기 때문에 r의 범위는 -1부터 0이 되겠지? 즉, r의 범위는 X와 Y의 관계가 정적일수도 있고 부적일수도 있으니 -1부터 1까지라는거야.

 

X와 Y가 정적 관계 일 때 : 0 ≤ r ≤ 1

X와 Y가 부적 관계 일 때 : -1 ≤ r ≤ 0

∴ -1 ≤ r ≤ 1

 

 이 r은 회귀 상수 처럼 다른 수치와 연산되는 것이 아닌 단위가 없는 지표(unitless index)이기 때문에 계수(coefficient)가 돼. 단위가 없이 그냥 방향이나 정도에 따라 관계성만 나타내는 놈이지. 그런데 이 놈을 피어슨이 고안했고 상관 관계를 나타내는 계수이기 때문에 '피어슨 상관 계수(correlation coefficient), r'로 불리는거야. (혹은 피어슨 적률 상관 계수) 이 상관 계수만 알면 X와 Y가 얼마나 큰 상관이 있는지, 어느 방향으로 상관이 있는지 알 수 있지! 아래의 고구마들 처럼 말야!

 

정적 상관 관계

 

 위의 고구마들은 정적 상관 관계를 나타내고 있기 때문에 2시에서 8시 방향으로 기울어져 있어. 그리고 고구마가 뚱뚱할 수록 상관관계가 낮아서 0에 가까워 지고, 고구마가 날씬할 수록 상관관계가 높아서 1에 가까워 지게되는 것이지. 반대로

 

 

 고구마가 10시에서 4시 방향으로 기울어져 있다면 부적 상관 관계를 나타내잖아? 고구마가 뚱뚱할 수록 상관 관계가 낮아서 0에 가까워 지고, 고구마가 날씬할 수록 상관 관계가 높아져서 -1에 가까워 지게 돼.

 

 고구마를 생각하면 상관 관계에 대해 쉽게 이해할 수 있겠지?

 

 그럼 다음 시간에는 피어슨 상관 계수를 계산해 보자구! 안뇽~