06-5 상관 계수를 변화시키는 표본 추출

 통계학을 공부하면서 잊으면 안되는 것! 우리는 미지의 모집단(population)이 가지고 있는 엄청난 양의 데이터를 분석할 수 없기 때문에 적당히 표본(sample)을 뽑아서(sampling) 조사를 한 다음, '음~ 모집단의 전체 자료를 가지고 분석을 하나, 표본집단을 가지고 분석을 하나 그게 그거구나~' 라는 생각을 갖고 '통계학 땡큐!!'를 외치면 된다고 했잖아.

 

 그리고 우리가 지금 상관 관계를 파악하기 위한 상관 계수, 특히 피어슨 상관 계수, r에 대해 배우고 있는데 이 r 또한 표본집단의 상관 계수라는거 잊지마! 만약 모집단의 상관 계수를 나타낸다면 그리스 알파벳 ρ(rho 라고 읽음)를 써서 나타내야 돼. 즉, 우리는 지금 r이 ρ와 얼마나 닮았느냐! 를 중요하게 생각해야 된다는거야. 기껏 구해 낸 r이 ρ과 다르다면 뭔 소용이 있겠어?

 

 그럼 r이 ρ와 달라질 수 밖에 없는 경우들을 살펴볼까?

 

-

 

1. 제한된 범위

 

 만약 모집단은은 뚜렷한 상관을 보이는데 표본집단은 그렇지 않다면?

 예를 들어 모 중학교에서 문해력 평가를 위한 시험을 만들었다고 해 볼게. 이 시험은 1학년 부터 3학년 전체 학생들을 대상으로 진행되었고, 결과를 분석해보니 문해력 평가 시험과 실제 문해력에는 상관이 있었어.

 

 

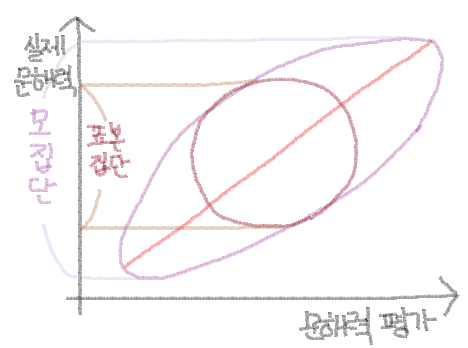
 문해력 평가 시험 점수와 실제 문해력 사이에는 0.76의 상관이 있었지. 0.7 이상이니까 뚜렷한 정적 선형 관계가 있다고 볼 수 있어. 그림만 봐도 전체 학생들의 고구마는 홀~쭉하지?

 그런데 이 중에서 2학년 학생들만을 뽑아서 살펴 보았더니, 상관이 있기는 했는데 0.28에 불과했어. 상관 관계가 있기는 한데.. 약한 정적 선형 관계에 불과 한 것이지. 끙~ 중2들은 참 모르겠는 존재야..

 

 앞서 추정 표준오차와 상관 계수의 관계를 살펴 봤을 때, 상관 계수 r²과 추정 표준오차 Sy.x²의 관계는

 

r² = 1 - Sy.x² / Sy² = 1 - {∑(Yi-Yh)²/(N-2)} / S²y = 1 - 예측 안된 분산 / Y 전체 분산 = 1 - 고구마의 뚱뚱한 정도 / Y 전체 분산

 

 라고 했었지? 그러니 당연히 Y의 범위가 줄어들면 Y의 분산이 줄어들면서 분모가 줄어들고, 분모가 줄어들면 상대적으로 분자가 커지면서 Sy.x²/Sy² 자체가 커지게 돼. 그럼 당연히 r² 또한 작아지게 되겠지.

 

 이 분석 결과를 토대로 한다면 이 문해력 평가 시험은 2학년 보다는 1학년이나 3학년 학생들을 대상으로 진행하는게 훨씬 더 효과적일거야. 그치? 그리고 이러한 분석을 했기 때문에 '2학년 학생들에게는 별 상관 관계가 없더라.' 라는 것을 알 수 있었고 말야. 전체를 보는 눈도 중요하지만 부분을 보는 눈도 중요한 것이지!

 

 만약 이 문해력 평가 시험을 만든 회사가 홍보에 쓰일 자료를 만든다면?! 절대로 2학년 학생만 따로 뽑아서 분석한 결과는 공개하지 않을거야. 전체 학생 혹은 1, 3학년 학생들을 가지고 분석한 자료를 통해 '우리 시험은 이~ 만큼 타당해요!' 라고 홍보하겠지. 안그래?

 

-

 

2. 극단적인 집단

 

 어떤 약물이 있다고 가정해 볼게. 이 약물은 안좋은 부작용을 갖고 있어. 하지만 일정량 이상을 복용하지만 않으면 부작용에 대한 위험도가 낮은 편이라 걱정하지 않아도 돼. 하지만 일정량을 넘겨 복용하게 되면 부작용이 발현 빈도가 갑자기 많아지는거야. 아래의 그림처럼 말야.

 

 

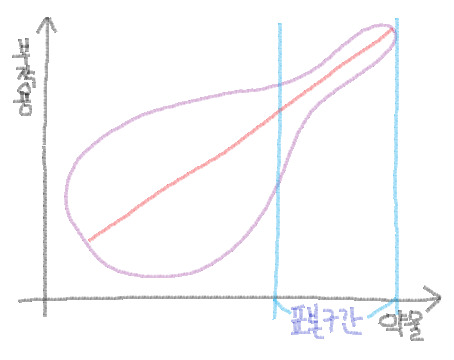
 전체 집단을 보면 정적 선형 상관 관계가 있기는 하지만 0.3 정도로 약한 관계만 나타내고 있어. 그리고 그림의 표본 구간 처럼 약물을 일정량 이상 복용한 집단에서는 상관이 0.8 이상으로 엄청 높지. 마지막으로 표본구간을 제외한 집단의 상관 관계는 0.1 로 무시해도 좋을 수준이야. 위 그림 전체만 놓고 보면 이 약물을 복용함으로써 부작용에 노출될 지도몰라. 하지만 일정량 이상으로 복용하지만 않으면 상관은 0.1로 매우 낮아지기 때문에 걱정하지 않아도 될 정도지! 그러나 일정량 이상으로 복용할 경우 부작용에 대해 걱정하지 않으면 안될 수준으로 높아지는 것을 볼 수 있어.

 표본집단의 고구마가 엄청 홀~쭉 하잖아? 상관이 높다는 말이지. 이런 경우에는 극단적인 집단이 전체 집단에 영향을 미칠 수 있어. 표본집단이 아닌 집단의 분산은 크지만 표본집단의 분산은 매우 작잖아. 이 표본집단이 전체에 영향을 미치게 되는 것이지.

 

 만약 내가 제약회사의 사장이라면 이 약물에 대해 어떻게 발표할까? 나라면 전체 집단의 데이터 보다는 일정량 이하의 약물을 복용한 경우에 한해서만 발표할 것 같아. 일정량 이상을 복용했을 때의 자료는 아예 공개하지 않는 것이지. 단, 약물에 '일정량 이상을 복용하지 마세요!' 라고 써 놓고, 일정량 이상 복용한 경우에 대한 책임을 소비자에게 묻는 것이지. 그럼 우리 제약회사에게는 아무 문제가 안생겨요! 땡큐 통계학!!

 

-

 

3. 결합된 집단

 

 죽음은 두렵지.

 얼마나?

 죽음은 아마 모든 사람들에게 두려울거야. 다만 그 두려움에는 차이가 있겠지. 어떤 심리학자는 초등학생들을 대상으로 죽음에 대한 공포를 알아보려 했어. 이런 연구를 왜 했을까? 킁..

 암튼 초등학생들의 정신 연령 수준과 죽음에 대한 공포를 조사했는데 결과는 아래와 같았어.

 

 

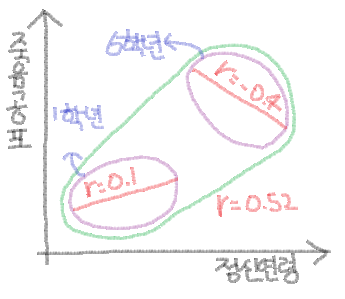
 먼저 1학년 학생들은 보면 정신연령이 낮을 수록 죽음에 대한 공포를 별로 느끼지 못했어. 아마 아직 어리니 죽음에 대한 개념도 부족할 것이고 별 관심도 없겠지. 태어난지 10년도 안되었으니까. 그래도 1학년 중에서도 정신연령이 높은 친구들은 대체로 죽음에 대한 공포도 많이 느꼈는데, 1학년 전체로 보면 상관 관계가 0.1로 매우 낮으니 정신연령과 죽음에 대한 공포가 상관이 거의 없다고 봐도 무방하겠지?

 다음으로는 6학년 학생들을 볼건데, 6학년에서는 오히려 정신연령이 높을 수록 죽음에 대한 공포가 낮아지는 것을 볼 수 있어. 오호라? 아마 죽음에 대한 막연한 불안감 보다는 죽음이 무엇인지 알게 되고 어떻게 하면 죽음을 피할 수 있는지 알게 되면서 줄어든 것이 아닐까? 특히 6학년 중에서도 정신연령이 높은 친구들, 즉, 좀 더 똘똘한 친구들 일수록 죽음에 대한 공포를 덜 느끼고 있어. -0.4 이면 뚜렷한 부적 선형 관계를 보인다고 할 수 있겠지? 참 신기한 조사네.

 (F.C. Jeffers, C.R. Nichols, and C. Eisdorfer, "Attitude of Older Persons to Death," Journal of Gerontology)

 

 암튼 1학년과 6학년을 살펴봤으면 초등학교 전체 학년 모두를 볼 필요가 있는데, 전체 학년에서는 1학년이나 6학년에서 보인 상관 관계와 달리 0.52로 뚜렷한 정적 선형 관계를 보이고 있어. 오호라?

 대체적으로 초등학생의 경우 정신 연령이 높을 수록 죽음에 대한 공포 또한 커지지만, 6학년의 경우에는 정신 연령이 높을 수록 죽음에 대한 공포가 낮다는 것이지.

 

 모집단이 정적 상관을 보인다고 해서 표본집단 또한 항상 정적 상관이 나타나지는 않는다는거야. 위의 사례처럼 말야. 다른 무수한 사례도 생각해 볼 수 있겠지? 인종 차별을 주제로 한 실험에서는 인종 전체에 대한 조사 결과와 흑인이나 아시안을 표본집단으로 한 조사 결과가 매우 다를거야. 

 

-

 

4. 극단적 점수

 

 모든 점수치들이 서로 고만 고만 한데, 어느 한 놈만 동떨어진 경우가 있어. 아래의 그림 처럼 말야.

 

 

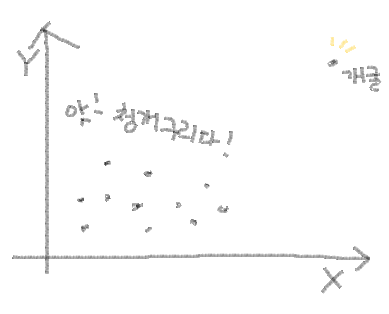
 이 경우 맨 오른쪽 상단에 위치한 청개구리 점수치만 없다면 다른 점수치들의 상관 계수가 0.51이지만 저 청개구리 같은 놈까지 넣어서 상관 계수를 구해보면 0.49라고 가정해 볼게. 하나의 점수치가 상관에 큰 영향을 미쳤지? 단 하나의 점수치 인데 말야. 별로 영향을 미친거 같지 않다고?

 여러분이 만약 어떤 연구를 진행하고 있는데, 상관 계수가 0.5를 넘겨야만 성공적인 연구가 된다고 생각해 볼까? 0.5만 넘기면 엄청난 연구비도 지원 받을 수 있고, 사회적으로도 인정 받고, 명예도 생기며, 주변 연구자들의 존경도 받을 수 있단 말야. 어? 그런데! 저 청개구리 같은 점수치 하나 때문에! 모든 것을 날리게 생겼어. 그럼 여러분들은 어떻게 할래?

 

 축구를 좋아하는 친구들이라면 위와 같은 경우를 많이 봤을거야. '리오넬 메시(Lionel Messi)'라는 아르헨티나 축구 선수로부터!

 

 

 위의 그래프들은 메시와 다른 선수들의 경기에서의 기록들을 나타낸 그래프야. 리오넬 메시만이 다른 점수치들과 동떨어져 상관 계수를 부셔버리고 있지. 상대 수비만 부셔버리는게 아니군!

 

 다만 표본이 충분히 크다면 하나 정도의 청개구리 점수치는 그렇게 큰 영향을 미치지 않을 수 있어. 하지만 표본이 작다면 하나의 청개구리는 판을 뒤집어 놓을 수도 있지!

 

-

 

상관과 인과

 

 상관 관계는 말 그대로 두 변인 간의 상관을 타나내는 말이야. '담배를 많이 피는 사람들이 폐암에 걸리더라. 그렇다면 담배와 폐암이 상관이 있겠군!' 이라는 추측을 통계학적 수치로 보자는 것이지. 그게 다야. 만약 상관 관계가 관측 되었다고 해서 '그렇다면, 담배는 폐암의 원인이군!' 이라고는 절대 말 할 수 없어. 상관 관계는 인과 관계의 정도를 나타내는 것이 아니니까. 앞서 배웠듯이 X로 부터 Y를 예측하든, Y로 부터 X를 예측하든 똑같았잖아? 그렇다면 담배를 펴서 폐암에 걸린다는 인과 관계를 뒤집어도 맞아 떨어져야 하는데 그렇지 않거든. 폐암에 걸린 사람들이 꼭 담배를 피는 것은 아니잖아.

 꽃향기를 맡으면 기분이 좋아지는데, 꽃향기와 좋은 기분이 서로 상관있기 때문이야. 반대로 좋은 기분과 꽃향기도 상관이 있겠지. 물론 꽃향기를 맡는 것 때문에 기분이 좋아질 수도 있어. 하지만 기분이 좋아질 때 갑자기 어디선가 꽃향기가 나타날까? 그럴 순 없어. 상관은 인과가 아니야.

 

 만일 X와 Y가 상관이 있다면,

 X는 Y의 원인이 될 수 있어.

 Y도 X의 원인이 될 수 있어.

 그런데,

 Z가 X와 Y의 모두의 원인이 될 수도 있어.

 

 담배(X)가 폐암(Y)의 원인일수도 있지만 유전적 요인(Z) 때문 일수도 있지. 어쩌면 Z가 더 중요할 수도 있고. 하지만 통계적 해석은 통계학자 마음대로지.

 

 이런 일들은 비일비재해. 통계학은 거짓을 말하진 않지만 거짓을 진실처럼, 진실을 거짓처럼 보이게는 할 수 있다는 이야기야. 학자의 양심이 무엇보다도 중요한 학문이 통계라는 것이지. 대중은 통계학자들이 만들어낸 수치만 보잖아? 그 수치가 어떻게 만들어졌는지는 아무도 관심이 없어. 오로지 자극적인 수치들만 본다고. 여러분이 통계학을 공부하면서 어떤 양심을 갖고 어떻게 판단하든 나는 상관하지 않아. (물론 선한 마음으로 선한 행동을 하면 좋겠지만..) 하지만 다른 사람들이 만들어낸 통계적 수치에 대해서는 과학자의 자세로 건설적인 의심을 하면서 세상에 감춰진 진실된 수치들을 보면서 살아갔음 좋겠어! 안뇽!

 

 p.s.

 특히 데이터 분석이라는 영역에서는 상관이 인과를 부셔버릴 수 있어. 사실 인과 관계를 밝히는 것은 굉장히 어려운 일이거든. 하지만 빅데이터의 영역에서는 우연일 수 없을 만큼의 거대한 경우들을 계속 만들어 낼 수 있거든. 아주 쉽고 간단하게. 그것이 인과 관계를 밝히는 것 보다 더 쉽다면 굳이 인과 관계에 목매달 필요가 있을까?