02-1 분포의 특징 : 빈도분포와 상대빈도분포

 과학자들은 어떤 현상을 연구할 때 관찰을 하지. 변인과 측정치들간의 관계를 알아야 하니까. 관찰을 하면 여러가지 수치들을 모을 수 있을꺼야. 그럼 이 수치들을 어떻게 정리할 수 있을까? '빈도분포(frequency destribution)' 혹은 '도수분포'가 답이 될 수 있지!

 

 빈도분포란 말 그대로 측정한 값을 특정 수치나 범위로 구분하고 얼마나 출현하는지를 나타내는거야. 동전 던지기를 예로 들어볼까? 동전을 던졌을 때 앞면이 나올수도 있고 뒷면이 나올수도 있어. 그것들을 관찰하고 측정한 다음 앞면이 얼마나 나왔고, 뒷면이 얼마나 나왔는지 보자는거지. 이를통해 빈도분포를 알 수 있으니까.

 

 어떤 학급에서 역사시험을 치뤘다고 가정해볼게. 10점 만점의 시험이었지. 10명의 학생들이 역사시험을 봤는데 결과는 아래와 같아.

 

학생	점수
A	8
B	10
C	9
D	7
E	9
F	8
G	7
H	6
I	8
J	7

 이제 이 관측된 수치들을 가지고 빈도분포를 알아볼거야. 일단 정렬을 해서 보기 좋게 만드는게 낫겠어. 점수가 높은 학생부터 낮은 학생 순으로 정렬해볼게.

 

학생	점수
B	10
C	9
E	9
A	8
F	8
I	8
D	7
G	7
J	7
H	6

 

 우리에게 중요한것은 학생의 이름이 아니라 학생이 취득한 점수이기 때문에 점수라는 관찰된 수치로 정렬하는게 빈도분포를 알기에 훨씬 더 유용할거야. 그치? 다음으로는 해당 점수를 취득한 학생이 몇 명이나 있는지 알아볼거야. 표를 보면 10점이 한 명, 9점이 두 명, 8점이 세 명, 7점도 세 명 마지막으로 6점은 한 명인 것을 알 수 있어. 표로 정리해볼까? 대신 학생이 누구인지는 중요하지 않기 때문에 점수만 가지고 표를 만들어 볼게.

 

점수	점수의 빈도분포
10
9
9	10점 : 1명
8	9점 : 2명
8	8점 : 3명
8	7점 : 3명
7	6점 : 1명
7	총 10명
7
6

 어때? 점수의 빈도분포를 보면 해당 점수를 취득한 학생이 몇 명인지 바로 알 수 있겠지? 이를통해 시험의 난이도가 어땠는지도 평가할 수 있을테고 말야.

 

 이번에는 A지역 80명의 미국인들에게 미합중국 대통령이 수행하는 정책에 어떤 생각을 갖고 있는지 알아보기로 했어. 국민들이 정책에 찬성하는지, 반대하는지 알아보기 위해서 말야. 질문에 대한 답변은 아래와 같아.

 

① 매우 찬성

② 찬성

③ 중립

④ 반대

⑤ 매우 반대

 

 오점척도라고 불리는 놈인데 많은 여론 조사 답변에 쓰이고 있지. 80명에게 물어봤을 때 아래와 같은 답변을 들을 수 있었어.

 

A지역의 여론조사
의견	f
매우 찬성	10
찬성	28
중립	12
반대	24
매우 반대	6
	N = 80

 위 표에서 f는 수치가 등장한 빈도(frequency의 약자)를 뜻하고 N은 전체 사례수를 뜻 해. 80명에게 물어봤으니 전체 사례수는 80이 되겠지? 그리고 현재 미합중국 대통령의 정책에 매우 찬성하는 사람은 9명, 찬성하는 사람은 30명, 중립적인 사람은 10명, 반대하는 사람은 25명, 마지막으로 매우 반대하는 사람은 6명인 것도 알 수 있어.

 어때? 이 표를 보니 왜 빈도분포가 필요한지 알겠지? 수치를 보는게 매우 편리해진 것을 알수 있으니까! 그럼 이제 B지역의 여론을 살펴볼까?

 

B지역의 여론조사
의견	f (빈도)
매우 찬성	40
찬성	112
중립	48
반대	96
매우 반대	24
	N = 320

 B지역의 여론조사를 얼핏보면 A지역에 비해 미합중국 대통력 정책에 찬성하는 사람들이 더 많아보여. 100명이 넘잖아! 정말일까?

 아니야. 사실 A지역과 B지역의 여론은 완전히 똑같아. 수치만 달라졌을 뿐이지.

 A지역을 보면 매우 찬성하는 사람이 80명 중에서 10명으로 8명 중 1명은 이 정책에 매우 찬성한다는 것을 알 수 있어. B지역은 320명 중의 40명, 즉 32명 중의 4명이 이 정책에 매우 찬성한다는 것을 알 수 있지. 32명 중의 4명과 8명 중의 1명은 다를까? 아니야! 같아! 둘 다 똑같이 8분의 1이기 때문이니까. 매우 찬성한다는 의견 뿐만 아니라 다른 의견들도 똑같은 비율을 가지고 있어.

 

 이렇듯 사례수가 달라지면 같은 내용을 담고 있다고 해도 자료에 대한 해석이 달라질 수도 있어. 인간은 기계처럼 빠르고 정확하게 계산할 수 없으니까! 그럼 어떡하지? '상대빈도분포(relative frequency distribution)'을 이용하면 돼!

 

 상대빈도분포는 말 그대로 빈도분포를 상대적인 비율로 나타내주는 분포야. 상대빈도분포를 이용하면 전체 사례수의 절댓값에서 오는 주관적인 느낌을 지울 수 있어.

 상대빈도분포의 기준은 100%, 즉 1이 돼. 전체를 1로 놓고 해당 수치의 빈도를 나타내는거야. A지역과 B지역의 여론조사 결과에서 상대빈도를 살펴볼까? 상대빈도는 상대빈도의 약자를 써서 'Rel f'라고 표기할게.

 

A지역의 여론조사
의견	f (빈도)	Rel f (상대빈도)
매우 찬성	10	0.125
찬성	28	0.35
중립	12	0.15
반대	24	0.3
매우 반대	6	0.075
	N = 80	1.000

B지역의 여론조사
의견	f (빈도)	Rel f (상대빈도)
매우 찬성	40	0.125
찬성	112	0.35
중립	48	0.15
반대	96	0.3
매우 반대	24	0.075
	N = 320	1.000

 빈도수(f)만 봤을 땐 달라보였는데 상대빈도(Rel f)와 같이 봤더니 완전히 똑같은 결과라는 것을 알 수 있었지! 상대빈도가 왜 중요한지 알겠지?

 

 사실 당연한 말이기도 했어.

 우리가 신문 기사나 TV 뉴스를 볼 때 어떤 조사를 보면 항상 '몇 명이 찬성한다.' 보다는 '몇 퍼센트가 찬성한다.'라고 표현하는 것을 볼 수 있잖아? 몇 명이 찬성하는지는 중요하지 않기 때문이야. 전체 사례수에 따라 상대빈도가 달라질 수 있으니까.

 

 이렇듯 빈도 분포는 수치를 기술하고 해석하는데 유용하다는 것을 알 수 있었어. 특히 빈도분포는 수치가 많을수록 더 중요하지! 한 번 살펴볼까?

 

 아래의 표는 내가 1부터 45까지 숫자 중에서 무작위로 생성한 100개의 숫자야. 난수라고도 하지.

17	31	32	7	43	35	44	42	29	11
13	18	22	14	15	35	35	30	27	30
38	18	21	31	11	38	29	42	39	37
28	28	8	30	29	38	30	29	24	17
18	33	5	19	42	25	23	37	45	23
38	17	18	13	37	20	12	42	20	8
1	28	20	28	31	9	6	18	15	25
25	20	6	30	37	4	19	12	20	1
28	18	16	16	43	45	4	42	18	30
40	25	33	21	19	28	35	44	20	40

 

 우리는이 표의 숫자들을 가지고 빈도분포표를 만들어 볼거야. 점수치가 45개로 너무 많기 때문에 '급간(class interval)'을 나눠놓고 빈도분포룰 살펴볼거야. 급간이란 점수치의 범위를 정해놓는 측정 척도의 한 구획이야. 1부터 5, 6부터 10, 11부터 15, 16부터 20, 21부터 25, 26부터 30, 31부터 35, 36부터 40 그리고 41부터 45의 총 9개의 범위로 나누어 놓자는거야. 45개는 너무 많으니까 9개로 줄이면 훨씬 더 보기 편하겠지? 아래의 표를 볼게.

 

급간	f	Rel f
1~5	5	0.11
6~10	6	0.13
11~15	9	0.20
16~20	21	0.47
21~25	10	0.22
26~30	17	0.47
31~35	10	0.22
36~40	11	0.24
41~45	11	0.24
	N = 100	1.00

 어때? 급간으로 나누어 놓으니 보기 편하지? 각 극간의 빈도와 상대빈도도 나타내어 봤어.

 거기에 추가로!

 이번에는 '누적빈도분포(cumulative frequency distribution)'와 '누적상대빈도분포(cumulative relative frequency distribution)'에 대해서도 알아볼거야. '누가빈도분포', '누가상대빈도분포'라고도 해. 누가 이름을 지었는지 참 길다!

 이름은 어려워 보이지만 의미는 어렵지 않아. '누적'이라는 뜻이 더해서 쌓아나간다는 뜻이잖아? 빈도나 상대빈도를 계속 더해나가면 그게 누적빈도나 상대누적빈도가 되는거야. 쉽지? 누적빈도는 'Cum f', 누적상대빈도는 'Cum Rel f'라고 표기해 볼게.

 

급간	f	Cum f	Rel f	Cum Rel f
1~5	5	5	0.05	0.05
6~10	6	11	0.06	0.11
11~15	9	20	0.09	0.20
16~20	21	41	0.21	0.41
21~25	10	51	0.10	0.51
26~30	17	68	0.17	0.68
31~35	10	78	0.10	0.78
36~40	11	89	0.11	0.89
41~45	11	100	0.11	1.00
	N=100		1.00

 단순히 더해서 쌓기만 하면 되니 어렵지 않지? 그럼 누적빈도나 누적상대빈도는 왜 필요할까? 빈도나 상대빈도는 딱 그 급간에 대한 정보만 얻을 수 있어. 하지만 누적빈도나 누적상대빈도는 해당 급간과 그 이하 급간에 속한 점수들의 수나 비율을 빠르게 알 수 있지!

 예를 들어11~15의 빈도만 보면 9라는 것 밖에는 알 수 없는데, 누적빈도를 보면 1~15의 빈도가 20이라는 것을 알 수 있지. 그치?

 시험 점수나 체중, 신장과 같이 연속된 수치들에 사용하면 참 편리하겠네!

 

 이제 빈도분포에 대해서도 알게 되었으니 실제 자료를 가지고 스프레드시트를 사용해서 빈도분포표를 만들어볼까?

 

 100명의 학생들이 어느 과목의 시험을 치뤘다고 가정해 볼게. 점수는 아래와 같아.

 

75	17	79	68	90	53	85	91	94	74
80	79	98	67	51	63	92	33	67	65
75	85	39	76	67	82	97	93	79	80
7	88	96	56	82	74	89	45	86	99
83	64	58	87	49	78	70	26	65	91
52	97	28	85	65	55	80	52	100	68
56	41	71	59	68	52	82	57	42	37
65	89	44	47	48	68	80	45	51	65
61	76	89	87	47	83	47	93	77	36
72	51	55	66	65	23	67	51	43	96

 여러분들은 위의 표를 복사해서 스프레드시트에 붙여넣기만 하면 돼. 그럼 아래와 같이 만들 수 있겠지?

 

 A2부터 J11까지 범위에 100명의 학생들의 시험 점수를 입력했어. 이 점수들을 가지고 빈도분포표를 만들어 볼거야. 빈도분포표에 급간, 빈도분포, 누적빈도분포, 상대빈도분포 그리고 누적상대빈도분포를 나타내어 볼게. 일단 양식을 만들어 볼까? 다만 급간을 나눌 땐 10점 단위의 범위로 나누어 줄거야. 총 10개의 급간이 나오겠지!

 

 빈도분포표의 양식이 완성되었어! 먼저 제일 간단해 보이는 빈도수부터 구해볼게.

 빈도수는 점수들에서 급간에 해당되는 점수들이 몇 개나 있는지 세어서 넣기만 하면 돼! 누가 세면 좋을까? 사람? 놉! 사람이 세지 않으려고 스프레드시트로 배우고 있는거잖아! 스프레드시트의 함수를 사용해서 급간에 해당하는 빈도를 구해볼거야.

 이때 사용할 함수는 'countifs' 함수야. countifs 함수는 여러 조건들을 동시에 만족하는 값을 셀 수 있는 함수지. countifs 함수를 사용하기 위한 수식은 아래와 같아.

 

=countifs(기준 범위1, 기준 조건1, 기준 범위2, 기준 조건2)

 

 기준이 되는 범위에서 기준을 만족하는 값을 찾아서 세어주는 유용한 함수지! 왜 기준 조건이 두 개 필요할까? 만약 A2부터 J11까지의 범위 중에서 0보다 큰 값을 찾고 싶다면 조건이 하나면 돼. 하지만 0보다 크고 10보다 작은 값을 찾고 싶다면 0보다 크다는 조건과 10보다 작다는 조건 두 개를 동시에 만족해야만 돼. 그래서 기준 조건이 두 개 필요한거야.

 '0보다 크다.'라는 조건은 ">0"과 같이 나타낼 수 있어. 비슷하게 '10보다 작다.'라는 조건은 "<10"과 같이 나타낼 수 있지! 만약 해당 수를 포함하고 있는 '이상'이나 '이하'를 나타내고 싶다면 '같다.'라는 의미의 등호(=)를 사용하면 돼.

 '0 이상.'이라는 조건은 ">=0"과 같이 나타낼수 있고, '10 이하.'라는 조건은 "<=10"과 같이 나타낼수 있어. 어렵지 않지?

 이제 A2부터 J11까지의 범위에서 countifs 함수를 사용해서 '0 이상.'과 '10 이하.'라는 두 조건을 동시에 만족하도록 수식으로 표현해 볼게.

 

=countifs(A2:J11, ">=0", A2:J11, "<=10")

 

 두 기준 조건의 범위는 A2부터 J11까지로 같기 때문에 기준 조건만 다른 것을 볼 수 있어. 이 수식을 첫 번째 급간에 적용해볼까?

 

 M2 셀에 수식이 입력되어있고 1이라는 값이 출력된 것을 볼 수 있어. 100개의 시험 점수 중에서 0이상 10이하 점수에 해당되는 점수는 단 하나 뿐 이라는거지.

 연습삼아서 M3 셀에 11이상 20이하 점수의 빈도도 구해볼까?

 

 M3 셀에는 11이상 20이하에 해당되는 점수의 개수가 출력 돼. 이번에도 한 명 뿐이 없네. 사실 시험 점수가 20점 이하라면 그 친구는 공부를 안했다고 봐도 되지. 마치 나의 학창 시절 시험 점수를 보는 것 같네..

 나는 어렸을 때 공부하는 것은 좋아했지만 시험보는게 너무 싫었어. 시험만 보면 평소에 알던 문제도 잘 풀어지지가 않고 그것 때문에 스트레스 받아서 더 못 풀고.. 악순환의 반복이었지. 수 주 동안 열심히 공부했던 것을 단 한번의 시험으로 평가한다는 것 자체가 맘에 들었지 않기 때문에 시험만 보면 스트레스를 받았어. 흑흑..

 

 암튼 나머지 급간들도 countifs 함수를 사용해서 구해보면,

 

 위와 같이 나타낼 수 있을거야. 마지막에 전체 사례수를 뜻하는 N은 저번 시간에 배운 sum 함수를 이용하면 쉽게 구할 수 있겠지? M2부터 M11까지의 합을 출력해주기만 하면 되니까! 까먹은 친구들을 위해 수식을 알려주면

 

=SUM(M2:M11)

 

 이렇게 나타낼 수 있어. 이제 바로 옆에 있는 누적빈도분포를 구해볼까?

 누적 빈도 분포 또한 전체 사례수를 구했던 것 처럼 더하기를 사용해야되는데, 연속된 여러 값이 아니라 단순하게 두 값을 더하는 것 뿐이라면 sum 함수를 사용하지 않아도 돼. 간단하게 키보드의 더하기 기호(+)를 사용하기만 하면 두 값을 더할 수 있지. 다만 첫 번째 누적빈도는 따로 더할 것 없이 급간에 해당되는 빈도를 그대로 넣어주면 돼. 누적할게 없으니까!

 두 번째 누적빈도부터는 첫 번째 빈도와 두 번째 빈도를 누적해서 넣어주어야 하지. 아래 처럼 말야.

 

 N3 셀에 0~10 급간의 빈도와 11~20 급간의 빈도를 더해서 넣어주었어. 0~10 급간 까지의 누적빈도는 N2에 출력되어 있고 11~20 급간의 빈도는 M3에 출력되어 있으니 그 둘을 합해주면 되겠지? 다음 누적빈도도 마찬가지야.

 

 0~20까지의 누적빈도가 N3에 출력되어 있고 21~30의 빈도가 M4에 출력되어있으니 두 셀을 더해주기만 하면 돼. 이 작업을 반복하면 아래와 같이 누적빈도분포를 완성할 수 있어.

 

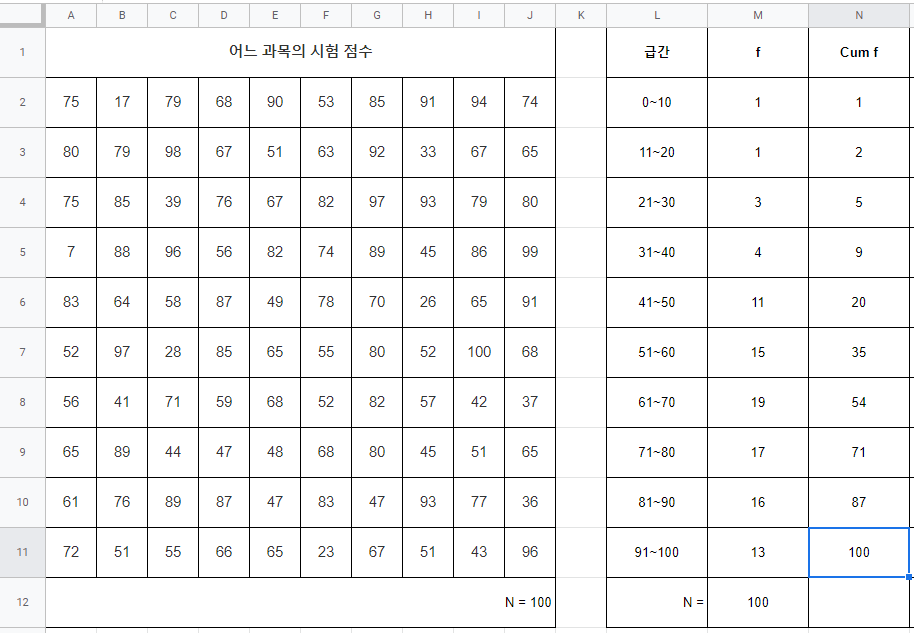
 누적빈도의 끝은 항상 전체 사례수와 같아야 돼. 당연한 말이겠지만.. 혹시라도 91~100까지의 누적빈도의 값이 100이 출력되지 않은 친구들은 잘못된 수식이 없나 확인해 봐!

 

 다음으로는 상대빈도분포를 구해볼거야. 상대빈도분포는 전체사례수에서 빈도가 얼마나 나타나고있는지에 대한 비율이었지? 빈도를 전체 사례수로 나눠주기만 하면 쉽게 구할 수 있어. 빈도는 구해놨으니 구해놓은 빈도값을 100으로 나누기만 하면 되겠네!? 나누기도 도하기를 할 때 처럼 간단하게 나누기 기호(/)를 사용하면 돼.

 

 0~10의 급간의 빈도는 1이기 때문에 상대빈도는 1을 100으로 나눈 값인 0.01이 될거야. 그치? 이런식으로 나머지 상대빈도와 상대빈도의 총합도 구해볼게!

 

 만약 위의 표 처럼 소수점 두 번째 자리 까지 깔끔하게 반올림되어 출력되기를 원하는 친구들은 상단의 툴바에서

 를 이용하면 돼.

 

 앞서 배웠듯이 상대빈도의 총합은 비율이기 때문에 100%를 뜻 하는 1이 나와야 돼. 만약 O2부터 O11까지의 범위 값들의 합이 1이 나오지 않은 친구들은 잘못된 수식이 없나 확인해 봐!

 

 다음으로는 누적상대빈도를 구하면 되는데, 누적상대빈도를 구하는 방법은 누적빈도를 구하는 방법과 완전하게 똑같아. 할 수 있겠지?

 

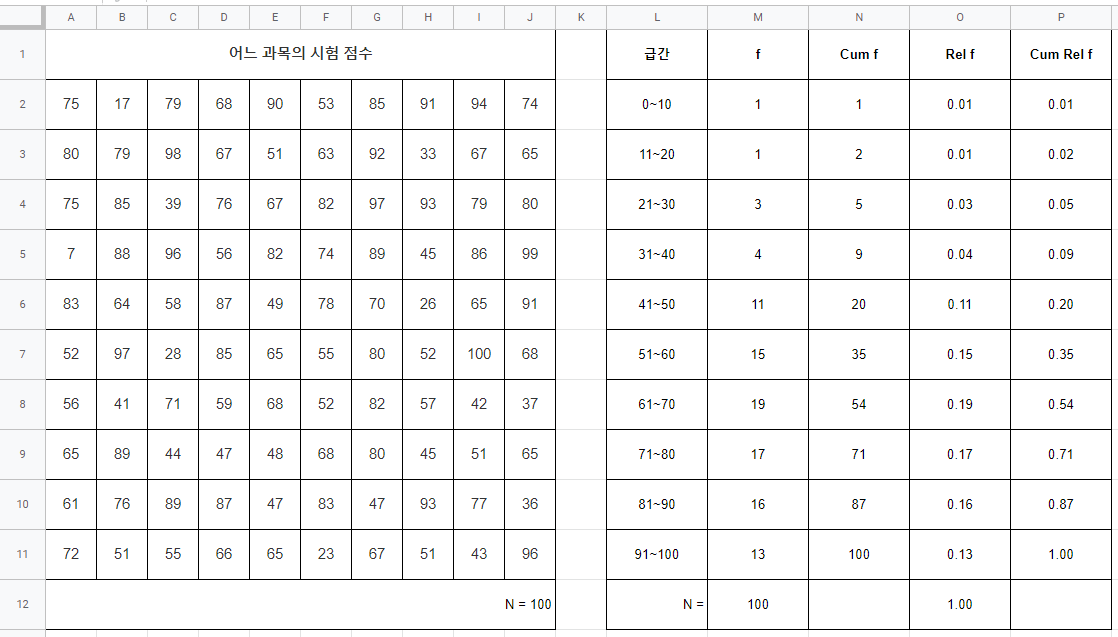
 누적상대빈도의 끝도 항상 1이 나와야 돼. 모든 급간의 상대빈도를 합한것이니 당연히 1이 나와야겠지!

 

 이로써 빈도분포표가 완성되었어! 스프레드시트의 힘을 빌리니 어렵지 않게 만들 수 있었네!

 왼쪽에 있는 점수표를 봤을 땐 이 시험이 얼마나 어려운 시험인지, 학생들이 시험을 잘 봤는지 못 봤는지 알기 쉽지가 않잖아. 하지만 오른쪽의 빈도분포표를 보니 71~80점을 맞은 학생이 가장 많은 것도 알 수 있고 대체로 학생들이 열심히 공부했다는 생각이 들어. 0점 맞은 학생도 없고 말야!

 

 굳이 길게 말하지 않아도 왼쪽의 점수표 보다 오른쪽의 빈도분포표가 점수치를 이해하는데 훨씬 도움이 된다는 것을 알 수 있을거야. 그리고 스프레드시트의 함수를 사용하면 쉽게 빈도분포표를 구할 수 있다는 것도 알게 되었고! 앞으로도 재미있는 통계적 수치들을 스프레드시트를 사용해서 구해보도록 할게! 안녕!

 

p.s.

 이 포스트에 쓰인 스프레드시트는

https://docs.google.com/spreadsheets/d/1GexpiJaqIfYQZQKR8k-9JQ82NzU9yaTBGklyjD40r3M/edit?usp=sharing 

02. 빈도분포와 상대빈도분포

 에서 열람할 수 있어! 스프레드시트 문서에 들어가면 아래 쪽에서

 

 '직접 만들어 보세요!' 시트를 선택할 수 있지!

 이 시트는 점수치와 빈도분포표의 양식만 만들어 놓은 시트이기 때문에 여러분들이 직접 빈 내용들을 채워 나가면서 공부해보길 바랄게! 그럼 진짜 안녕!