01-3 시그마와 평균 : 합의 기호 ∑와 평균 그리고 연산

 앞서 통계가 무엇인지, 통계를 왜 배워야 하는지 배웠어. 그럼 이제 통계적 기법들을 위한 방법을 배워볼까?

 아참, 이제부터는 구글 스프레드시트를 활용하면서 본격적으로 시작해 볼게!

 

 먼저 합의 기호를 배울거야. 히랍어 대문자 '∑'라고 쓰고 '시그마(sigma)'라고 읽어. 고등학교 때 배운적 있지? 만약 이 글을 읽는 친구가 시그마를 모른다고해도 괜찮아. 내가 알려줄거니까!

 

 일단 합의 기호가 왜 필요한지부터 알아야겠지?

 우리가 접하게 될 자료들은 하나의 수치가 아니라 여러 수치들이 뭉쳐있는 자료 덩어리들을 접하게 될거야. 특정 집단이 주어진다면 특정 집단의 모든 수치들을 다뤄야 하는거지. 중요한 것은 '모든'이라는 단어야.

 

 앞서 배웠던 모집단과 표본집단을 떠올려봐. 모집단은 대부분 너~무~나 많기 때문에 모집단의 전체 수치들을 다루기란 사실상 불가능해. 전세계 모든 ADHD 환자들에 대한 정보를 다 수집한다고? 오노! 그럴순 없어. 하지만 모집단에서 무작위로 표본추출한 표본집단이라면? 표본집단은 추론 통계를 위해 추출한 집단이기 때문에 사례수가 모집단에 비하면 매우 적을거야. 표본집단이 가지고 있는 모든 수치를 다룰 수 있을 만큼 적겠지. 우리는 표본집단과 같이 파악 가능하고 계산 가능한 집단의 수치들을 컴퓨터 기술을 통해 다룰 수 있어. 그 때 필요한 기호 중 하나가 바로 시그마(∑)야.

 

 쉽게 이해하기 위해 아래의 표를 먼저 볼게.

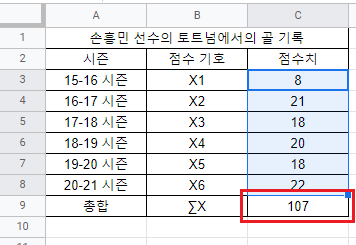
손흥민 선수의 토트넘에서의 골 기록
시즌	점수 기호	점수치
15-16 시즌		8
16-17 시즌	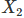	21
17-18 시즌		18
18-19 시즌	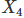	20
19-20 시즌		18
20-21 시즌		22

(편의를 위해 텍스트에서는 변인의 밑수를 일반 숫자로 대체하여 설명합니다.)

 

위의 표는 실제 손흥민 선수의 기록이야. 16-17 시즌 부터의 활약이 돋보이네!

 그리고 점수 기호는 '변인(variable)'을 나타내기 위해 가장 많이 쓰이는 X로 나타냈어. 프로그래밍을 배운 친구들이라면 '변수(variable)'의 개념을 떠올리면 돼. X4는 18-19 시즌의 골 기록을 나타내는 변인이 되는거야. 어렵지 않지?

 

 이제 우리는 손흥민 선수가 토트넘에서 한 시즌당 평균 몇 골을 넣었는지 알고 싶어졌어. 어떻게 알 수 있을까?

 간단해. 모든 득점수의 합을 시즌의 횟수대로 나누면 돼. 총 여섯 시즌 동안의 기록이니까 모든 득점수를 합한 다음 6으로 나누면 되는거야. 수식으로 정리하면,

 

평균 = 모든 점수들의 합 / 점수들의 수

(프로그래밍에서 '/' 기호는 '÷'를 뜻 함. '/'를 기준으로 앞에 오는 것이 분자, 뒤에 오는 것이 분모이기 때문)

 

 가 되겠지. 위의 표에서는 점수가 '득점수'가 되는 것이고. 그런데 '모든 점수들의 합'이라는 말이 너무 길잖아? 그래서 우리는 이제부터 '모든 점수들의 합'을 '∑(시그마)'라고 할거야. ∑ 자체가 합의 기호이기 때문에 가능하지! 그리고 만약 위와 같이 모든 변인 X들의 합을 나타내고 싶다면 '∑X'라고 표현하면 돼. 끝으로 '점수들의 수'는 N으로 표현할 수 있어. 이제 평균을 구하는 수식을 기호들을 사용해서 다시 표현해 볼까?

 

평균 = ∑X / N

 

 어때? 훨씬 간단해졌지?

 사실 변인 X들의 합을 더 자세하게 나타내려면

 이런 식으로 나타내야 돼. Xi에서 i를 1부터 N까지 1씩 증가시키면서 더한다는 뜻이야. 정리하면,

와 같지. 쉽게 말해서 X1부터 XN까지 모든 변인들의 점수치를 다 더하라는 뜻이야. 손흥민 선수가 토트넘에서 6시즌 동안 득점한 총 득점수를 구한다고 하면

 이렇게 나타낼 수 있어. i가 1부터 6까지 1씩 증가하면서 더하라는거지. 그리고 실제 기록에 대입해보면

와 같이 나타낼 수 있어. 6시즌 동안 107득점이라니! 굉장한걸?

 만약 한 집단의 모든 점수치들을 더한다고 한다면 기호는 생략될 수 있어.

 나는 앞으로 텍스트로 설명할 땐 '∑X'로 나타낼거야. 그래도 여러분들을 찰떡같이 알아듣고 '집단의 모든 점수치들을 더한 것이구나!' 라고 알 수 있겠지?

 

  이제 합의 기호는 알았으니 스프레드시트에서 어떻게 하면 점수치들을 더할 수 있는지 알아봐야겠지? 스프레드시트에서는 정말 쉽게 값들의 합을 알아낼 수 있어. 먼저 스프레드시트에 데이터를 입력해야돼.

 그리고 내가 합하고자 하는 데이터들을 선택해야 돼. 점수치들을 선택하면 되겠지?

 

 

 그리고나서 상단의 아이콘 중에서 함수를 적용할 수 있는 시그마 기호 아이콘을 찾아서 누르고 'SUM'을 선택하면!

 내가 선택한 데이터들의 합을 더할 수 있는 수식이 그 다음 행에 자동으로 입력돼!

 

 수식의 내용은 SUM이라는 함수를 통해 C3부터 C8까지의 값을 더하라는 내용이야. 수식이 입력된 상태에서 키보드 엔터(enter)키를 누르면 계산된 값을 볼 수 있어.

 

 어때? 참 쉽지?!

 몇 번의 클릭 만으로 내가 합하고자 하는 값들을 구할수 있으니 엄청 편리하네!

 

 마지막으로 우리가 배운 기호를 활용해서 나타내보면

 

 이렇게 나타낼 수 있어. ∑X는 X 변인들의 총합을 뜻해.

 이제 ∑에 대해 알겠지? 총합을 구할 수 있다면 평균도 구할 수 있을거야! 한 번 구해볼까?

 

 평균, 정확히는 모든 점수들의 합을 점수들의 수로 나눈 '산술 평균(arithmetic mean)'을 구해볼거야. 우리가 흔히 쓰는 평균이라는 용어는 산술 평균을 뜻하는데, 평균에는 산술 평균 말고도 기하 평균(geometric mean)이나 조화 평균(harmonic mean)등이 있어. 기하 평균이나 조화 평균에 대해서는 필요하면 그때가서 다시 설명해줄게! 암튼 평균을 mean이라고 한다는 것만 알고 있으면 돼.

 잉?! 평균은 average가 아니었나?! 맞아. average나 mean이나 한국어로 번역하면 둘 다 평균이니까. 하지만 average는 보통 산술 평균을 의미하고, mean은 수학적 평균으로 산술 평균이나 기하 평균 혹은 조화 평균등을 의미하는 것이지. 용어를 한 번에 너무 많이 배우면 헷갈리기 마련이니 용어에 대한 정리는 배우면서 차차 해나가도록 할게!

 

 X 변인들의 평균 또한 기호로 나타낼 수 있어.

 

 위와 같이 쓰고 '엑스 바'라고 읽어. 하지만 X바는 컴퓨터로 입력하기가 어렵기 때문에 앞으로 텍스트로 설명할때에는 mean을 뜻하는 'm'이라고 할게.

 

 이제 평균에 대한 기호도 익혔으니 평균을 구하는 방법을 새로 나타낼 수 있을거야. 

 

 X바는 평균을, ∑X는 X 변인들의 합을, 마지막으로 N은 X 변이들의 수를 뜻 해.

 어때? 기호로 나타내니까 굉장히 간단하게 보이지? 텍스트로 나타내면

 

 m = ∑X / N

 

 으로 나타낼 수 있겠네. 그놈이 그놈이니 어떻게 나타내든 잘 알아줬음 좋겠어!

 이제 스프레드시트로 평균을 구해볼까?

 

 평균을 구하는 것도 값들의 합을 구했던 것과 같이 굉장히 간단해. 내가 평균을 구하고자 하는 값들을 선택한 다음 상단의 아이콘 중에서 시그마 모양의 함수 아이콘을 찾고 'AVERAGE'만 선택하면 되지!

 

 AVERAGE를 선택하면 내가 선택한 값들의 평균값을 구할수 있는 수식이 바로 다음 행에 자동으로 생성돼. 그런데 우리는 앞서 SUM을 선택해서 총합을 구해놨었기 때문에 셀을 정해주지 않으면 우리가 구했던 총합에 덮어씌워지게 될거야.

 

점수치들을 선택하고 AVERAGE를 선택하면 총합이 구해져있는 C9셀에 덮어씌워지게 돼!

 그러면 안되겠지? 값을 덮어씌우지 않기 위해 C9셀 바로 밑의 행인 C10에 평균을 구해보자구. 방법은 간단해. C10을 선택하고 함수 아이콘에서 AVERAGE를 클릭하면 돼. 혹은 C10셀의 수식 입력창에 '=AVERAGE()'를 직접 입력하는 방법도 있어.

 

 AVERGAGE() 함수를 사용하면 소괄호 안의 값들의 평균을 구할 수 있어. 소괄호 안에 내가 구하고자 하는 값들의 셀을 직접 입력해도 되고, 아니면 마우스를 사용해서 값들을 선택해 주어도 돼.

 

 만약 직접 입력한다고 C10의 수식은 'C3부터 C8까지의 값들'이라는 뜻의 'C3:C8'를 사용해서 입력할 수 있어.

 

=AVERAGE(C3:C8)

 

 그리고 키보드의 엔터키를 누르면 17.83이라는 수치가 출력될거야. 한 시즌당 거의 18골을 넣었다니.. 손흥민 선수는 참 대단한걸?!

 

 이제 합의 기호 시그마를 사용해서 점수들의 합을 나타내는 방법, 그리고 스프레드 시트를 통해 계산하는 방법에 대해 잘 알겠지? 그리고 평균을 구하는 방법도 말야.

 

 그럼 마지막으로 합의 기호를 사용한 연산에대해 알아볼게.

 

-

 

 합의 기호를 사용한 연산

 

 1. '변인에 어떤 상수를 곱한 것들의 합'은 '변인의 합에 어떤 상수를 곱한 것과 같다.'

 말이 아리송해 보이네. 무슨 뜻일까? 1부터 5까지의 합은 얼마일까? 15지. 이제 1부터 5까지의 숫자에 각각 2를 곱해볼거야. 그럼 1, 2, 3, 4, 5는 2, 4, 6, 8, 10이 될거야. 그리고 2, 4, 6, 8, 10의 합은 30이 되겠지. 그치?

 이번에는 순서를 반대로 해볼거야. 먼저 1부터 5까지의 합을 구한 다음 2를 곱해보는거지. 1부터 5까지의 합은 15니까 여기에 2를 곱하면 30이 되겠네?

 즉, 변인에 상수를 곱해서 합하나 변인의 합에 상수를 곱하나 그놈이 그놈이라는 소리야. c가 상수이고 X가 변인이라고 하면

 

 이렇게 나타낼 수 있어. 잊지마!

 

 2. '어떤 상수를 N번 더한 것'과 '어떤 상수에 N을 곱한 것'은 같다.

 어떻게 보면 당연한 말이긴 한데.. 1을 다섯 번 더한 것과 1에 5를 곱한 것은 당연히 같겠지? c가 상수라면 아래와 같이 나타낼 수 있어.

 

 간단하지?

 

 3. '다른 두 변인을 더해서 합한 것'과 '다른 두 변인의 합을 더한 것'은 같다.

 이번에는 X변인 뿐만 아니라 Y변인도 있다고 해볼게. X변인들과 Y변인들을 각각 더한 다음 합을 구한 것과 X변인들의 합과 Y변인들의 합을 더한 것이나 같다는 말이야.

 예를 들어볼까?

 X변인들에는 1, 2, 3이 있고 Y변인들에는 4, 5, 6이 있다고 해볼게. 첫 번째 X변인인 1과 첫 번째 Y변인인 4를 더할거야. 5가 되겠네. 그 다음에는 2와 5를 더할거야. 7이지. 마지막으로 3과 6을 더하면 9가 돼. 이제 이것들을 다 합하면? 5와 7을 그리고 9를 합하면 21이 돼.

 이번에는 반대로 X변인들을 다 합해줄거야. 1, 2, 3을 합하면 6이 되겠지? 그리고 Y변인들도 다 합해볼거야. 4, 5, 6을 합하면 15가 되네. 마지막으로 두 변인들의 합을 더해줄거야. 6과 15를 더하면 21이 되는거지. 각각의 변인들을 더해서 합하나, 변인들의 합을 더하나 그게 그거지? 기호로 나타내면

 

 와 같이 나타낼 수 있어. 어렵지 않지? 마지막으로,

 

 4. '∑X²는 제곱된 점수들의 합'이고 '(∑X)²는 점수들의 합을 제곱한 것'이다.

 앞으로 제곱을 정말 많이 쓸텐데 헷갈리면 안돼. 보기엔 비슷하지만 ∑X²과 (∑X)²는 서로 다르니까 조심해야돼.

 만약 X변인들이 1, 2, 3이라면 제곱된 점수들의 합은 1²(=1)과 2²(=4) 그리고 3²(=9)을 합한 값인 14가 되는 것이고, 점수들의 합을 제곱하면 1, 2, 3을 합한 9에 제곱을 해서 81이 되는 것이지. 어때? 14와 81은 엄청나게 큰 차이를 갖고있지? 숫자가 이렇게 작은데도 큰 차이를 보이고 있다면, 나중에 더 큰 숫자들로 계산해 본다면 훨씬 더 많이 차이나게 될거야.

 

 합의 기호 시그마와 연산 방법만 알아도 되게 많은 것들을 할 수 있어! 앞으로 재미있는 계산들이 많이 기다리고 있으니 배운 내용을 적용해서 풀어볼까? 하핫!