03-2 중심경향의 지표 : 중앙값과 최빈값

 다음 살펴볼 집중경향의 지표는 중앙값와 최빈값이야. 먼저 중앙값부터 살펴볼까?

 

 중앙값(median) 혹은 중앙치는 말 그대로 점수치들 중에서 제일 중앙에 있는 놈을 뜻 해. 다섯 명의 시험 점수를 정렬했을 때 중앙에 위치한 사람의 점수가 중앙치가 돼. 쉽지? 예를 들면 정렬된 점수치들이 '1, 3, 5, 7, 9'와 같다면 중앙에 있는 5점이 이 점수치들의 중앙값이 되는거야.

 중앙값이 위치한 곳은 전체 점수치의 개수에서 1을 더한 다음 2로 나누어주면 쉽게 구할 수 있어. 5개의 점수가 있다면 5에서 1을 더한 6을 구한 후 2로 나눠주면 돼. 3이 나오지? 세 번째 위치한 점수치가 중앙값이는 뜻이야. 전체 점수치의 개수를 N이라고 했을 때 좀 더 간단하게 수식으로 나타내면,

 

 (N이 홀수일 때) 중앙값이 위치한 순서 : (N+1) / 2 

 

하지만 점수치가 짝수개라면?!

 여섯 명의 시험점수를 정렬했을 땐 세 번째 점수와 네 번째 점수 사이가 중앙이 될거야. 그럼 세 번째 점수와 네 번째 점수 중에서 어떤 것을 중앙값으로 하면 좋을까? 대~충~ 하나를 고를까? 안돼! 중앙에 위치한 두 값들을 가지고 새로운 중앙값을 만들어야돼! 평균을 이용해서 말야!

 

 점수치의 개수가 짝수일 땐 중앙값이 두 개 일수밖에 없어. 그럴 땐 이 두 값의 평균을 중앙값으로 정하면 돼. 만약 정렬된 점수치들이 '2, 4, 6, 8'과 같다면 중앙에 위치한 두 값인 4와 6의 평균인 5를 중앙값으로 하는거지! 참 쉽지?

 그럼 점수치의 개수가 짝수일 때의 수식을 생각해 볼까? 먼저 중앙에 위치한 두 값의 순서를 구해야 돼. 하나는 전체 개수에서 2를 나눠주면 되고 다른 하나는 전체 개수에서 1을 더한 후 2로 나눠 주면 돼. 그리고 그 둘의 평균을 구하기만 하면 되지! 점수치의 전체 개수를 N이라 했을 때,

 

 (N이 짝수일 때) 중앙값이 위치한 순서들 : N/2와 (N+1)/2

 

 로 표현할 수 있겠어.

 이제 중앙값을 구해낼 수 있겠지?

 

 그런데!

 구글 스프레드시트를 이용하면 엄청 쉽게 중앙값을 구할 수 있어!

 

 아래와 같은 점수치들의 중앙값을 구하고 싶다면

함수를 뜻하는 시그마(∑)아이콘을 선택한 다음 '통계'에 있는 함수 중에서 중앙값을 뜻 하는 'MEDIAN'을 찾기만 하면 돼. 알파벳 순이니까 M이 나오는 곳 까지 쭉 내리면 금방 찾을 수 있어.

 

 그럼 자동으로 A2부터 A6까지의 범위에서 중앙값을 찾아주는 수식이 입력될거야.

 

=MEDIAN(A2:A6)

 

 그리고 이 함수를 통해 중앙값을 찾아보면

 

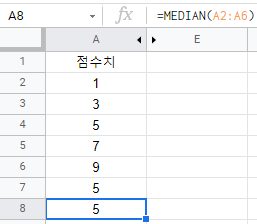
 A8셀에 중앙값인 5가 출력되는 것을 볼 수 있어! 진짜 쉽다! 사실 '통계'에는 우리가 앞으로 배울 통계와 관련된 유용한 함수들이 많이 있어. 다른 것들도 나중에 살펴볼게!

 

 MEDIAN 함수를 이용하면 전체 개수가 홀수 개이든, 짝수 개이든 알아서 중앙값을 찾아 줘. 이번에는 B2부터 B5까지 총 네 개의 점수치를 가지고 중앙값을 구해볼게.

 

 마찬가지로 MEDIAN 함수를 사용해서 수식으로 나타내었더니 중앙값으로 5를 출력해주네! 중앙에 위치한 4와 6의 평균값이 제대로 출력되었어! 야호!

 

 다음으로는 최빈값에 대해 살펴볼게.

 최빈값(mode)은 점수치들 중에서 가장 빈번하게 나타나는 놈을 뜻 해. 만약 점수치들이 '1, 2, 2, 3, 3, 3, 4, 4, 4, 4'와 같다면? 1이 한 개, 2가 두 개, 3이 세 개, 4가 네 개로 4가 가장 많이 등장하는 것을 알 수 있어. 그럼 4가 이 점수치들의 최빈값이 되는거야. 진짜 쉽지?

 

 어? 그런데 만약 최빈값이 둘 이라면?

 만약 점수치들이 '5, 6, 6, 7, 7, 7, 8, 8, 8'과 같다면 7과 8이 각각 세 번씩 등장하기 때문에 동률이 돼. 그럼 이 때 어떤 놈을 최빈값으로 해야 될까? 중앙값을 구했던 때 처럼 둘의 평균을 최빈값으로 할까?

 안돼! 멈춰! 동률인 최빈값이 관측되어도 따로 무슨 짓을 하지 않아도 돼. 둘 다 최빈값이기 때문이야. 둘 이상의 최빈값이 관측되어도 그놈들 전부 최빈값이 되는거야. 위와 같은 점수치들에서는 7과 8 둘 다 최빈값이 되는거지. 최빈값이 둘 이라면 양봉적(bimodal), 둘 이상이라면 다봉적(multimodal)이라고 할 수 있어.

 

 최빈값은 따로 구하는 공식이 없기 때문에 눈으로 세야만 해. 점수치가 많으면 굉장히 곤란하겠지? 하지만 구글 스프레드시트를 사용하면 쉽게 최빈값을 구할 수 있어! 중앙값을 구할 때와 마찬가지로 통계 함수 중에서 최빈값을 뜻 하는 MODE를 찾아주기만 하면 돼.

 

 MODE를 찾아서 누르면 자동으로 내가 정한 범위에서 최빈값을 찾아주는 함수가 입력될거야. 만약 C2부터 C11까지의 셀에서 최빈값을 찾는다고 하면,

 

=MODE(C2:C11)

 

 가 입력될거야. 만약 '1, 2, 2, 3, 3, 3, 4, 4, 4, 4'가 입력되어있는 C2부터 C11까지의 범위를 선택하고 최빈치를 C12에 찾는다고 하면 아래와 같이 출력될거야.

 

 4가 네 번으로 가장 많이 등장하기 때문에 최빈값이 4로 출력되었어. 야호!

 다음으로는 최빈값이 둘 이상일 때를 살펴볼까? D2부터 D10까지의 범위에 '5, 6, 6, 7, 7, 7, 8, 8, 8'이 입력되어있을 때 D11에 최빈값을 출력해 볼게. 마찬가지로 MODE함수를 이용하면 되겠지?

 

 앗! D2부터 D10까지의 최빈값을 7과 8로 두 개 인데 D11셀에 7 하나밖에 출력되지 않았어! MODE 함수는 하나의 최빈값밖에는 출력할 수 없기 때문이야. 만약 두 개 이상의 최빈값을 출력하고 싶다면 MODE 함수가 아니라 MODE.MULT 함수를 사용해야 돼.

 

 MODE.MULT 함수를 사용해서 D11셀에 D2부터 D10까지의 범위 중 최빈값을 찾아내려면

 

=MODE.MULT(D2:D10)

 

 와 같이 나타내면 돼. 그럼 아래와 같이 D11셀에 최빈값이 출력될거야.

 

 앗! 그런데 D12셀에도 값이 출력된 것을 볼 수 있어! 또 다른 하나의 최빈값인 8이 출력되어있네! MODE.MULT 함수를 사용했기 때문에 여러개의 최빈값을 출력한 것이지! 만약 최빈값이 하나라고 해도 MODE.MULT 함수는 정상적으로 동작 해. 그러니 최빈값이 한 개 인지, 두 개 이상인지 모르겠지만 모든 최빈값을 다 찾고자 한다면 MODE 함수 보다는 MODE.MULT 함수를 사용하는게 적절하겠지? 당연히 최빈값이 하나라면 MODE 함수를 사용해도 괜찮지만 말야.

 

 스프레드 시트를 사용해서 쉽게 중앙값과 최빈값을 구하는 방법에 대해 알아봤어. 만약 위 스프레드 시트 문서를 참고하고 싶다면

https://docs.google.com/spreadsheets/d/1o7wQSQChxdl0_kwiBeaLgs1GLE6mokjHrVjx_g3VTSg/edit?usp=sharing 

03-2 중심경향의 지표 : 중앙값과 최빈값

 이 문서를 열람하면 돼!

 

 -

 

 중심경향의 지표인 평균과 중앙값 그리고 최빈값에 대해 배워봤어. 어때? 각자의 개성이 있지?

 점수치들이 어떻게 구성되어있느냐에 따라서 집단을 대표하는 중심경향에 평균이 적합할 수도 있고, 중앙값이 적합할 수도 있고, 최빈값이 적합할수도 있어. 만약 분포가 아래와 같다고 해볼게.

 

분포	평균	중앙값	최빈값
1, 3, 5, 7, 9	5	5	1, 3, 5, 7, 9
1, 3, 5, 7, 99	23	5	1, 3, 5, 7, 99
1, 3, 5, 7, 999	203	5	1, 3, 5, 7, 999

 

 위와 같이 평균은 어느 한 점수치에 의해 영향을 굉장히 많이 받을 수 있어. 반면 중앙값은 그렇지 않지. 그리고 최빈값은.. 사실 특정한 상황 외에는 별 쓸모가 없어. 딱 봐도 그렇지?

 

 물론 평균이나 중앙값 그리고 최빈값이 같을수도 있어. 점수치들이 '1, 2, 2, 3'과 같다면 그렇게 되겠지? 그림으로 살펴볼게.

 

평은 평균, 중은 중앙값 그리고 최는 최빈값

 위와 같은 분포를 나타내고 있다면 평균과 중앙값 그리고 최빈값이 같을 수 있지. 우리가 배우게 될 인간과 관련된 점수치들은 주로 위와 같이 나타나게 될거야. 신장(키)이라던가 분당 맥박수, 눈 깜빡임 횟수 등 여러가지 것들이 이런 분포를 보일거야. 그런 것들은 나중에 살펴보기로 하자구!

 다음으로는

 

평은 평균, 중은 중앙값 그리고 최는 최빈값

 위와 같은 분포를 보일수도 있어. 남성과 여성의 신장등이 위와 같은 분포를 가질 수 있을거야. 점수치가 낮은 최빈치는 여성의 신장, 점수치가 높은 최빈치는 남성의 신장이 될 수 있겠지? 그리고 평군과 중앙치가 같을수도 있을것이고.

 다음으로는

 

 위와 같은 분포를 보일수도 있는데, 이 분포는 부적 편포도라고도 해. 기억나지?

 암튼 우와 같은 분포에서는 평균과 중앙값 그리고 최빈값이 모두 다른 상황이야. 저번에 시험 점수 가지고 빈도분포표 만들었을 때 이와 같은 모습의 분포를 볼 수 있었을거야. 시험이 쉬워서 대부분의 학생들이 좋은 점수를 받는다면 이런 분포를 볼 수 있지!

 

 이렇듯 분포에 따라 집단을 대표하는 집중경향의 지표를 어떤 것으로 해야하는지 고민이 생길 수 있어. 집중경향에 대해 공부하기 전에 평균만 알고 있었던 때가 더 좋았던 것 같기도 해. 아는게 평균밖에 없으니 고민하지 않아도 되니까. 하핫! 그래도 너무 걱정은 하지마! 우리가 다룰 사화과학, 과학분야에서는 대부분의 상황에서 평균을 집중경향의 측정치로 사용하니까! 평균을 집중경향의 측정치로 사용하는 여러가지 이유가 있겠지만 가장 중요한 이유는 많은 다른 통계 절차에 평균이 요구되기 때문이야.

 그래도 중앙값이나 최빈값도 상황에 따라 쓰일 수 있다는 것은 잊지 말구! 특히 변산성이 큰 경우에는 평균의 힘이 약해질 수 있겠지? 마이클 조던의 일화처럼 말야! 많은 경제학자들은 경제적 지표와 같이 극단의 차이가 많이 나는 경우에는 평균보다는 중앙값이 더 적절한 집중경향의 지표라고들 말해.

 

 앞으로는 평균만 생각하지 말고 우리가 배운 집중경향의 지표들을 적절하게 생각하면서 살았으면 좋겠어! 안녕~!